Activity: Subsets

Please read Introduction to Sets first!

This activity investigates how many subsets a set has.

What is a Subset?

A subset is a set contained in another set

It is like you can choose ice cream from the following flavors:

{banana, chocolate, vanilla}

You could choose any one flavor {banana}, {chocolate}, or {vanilla},

Or any two flavors: {banana, chocolate}, {banana, vanilla}, or {chocolate, vanilla},

Or all three flavors (no that isn't greedy),

Or you could say "none at all thanks", which is the "empty set": {}

 

Example: The set {alex, billy, casey, dale}

Has the subsets:

  • {alex}
  • {billy}
  • etc ...

It also has the subsets:

  • {alex, billy}
  • {alex, casey}
  • {billy, dale}
  • etc ...

Also:

  • {alex, billy, casey}
  • {alex, billy, dale}
  • etc ...

And also:

  • the whole set: {alex, billy, casey, dale}
  • the empty set: {}

Now let's start with the Empty Set and move on up ...

The Empty Set

How many subsets does the empty set have?

You could choose:

But, hang on a minute, in this case those are the same thing!

So the empty set really has just 1 subset (which is itself, the empty set).

It is like asking "There is nothing available, so what do you choose?" Answer "nothing". That is your only choice. Done.

A Set With One Element

The set could be anything, but let's just say it is:

{apple}

How many subsets does the set {apple} have?

And that's all. You can choose the one element, or nothing.

So any set with one element will have 2 subsets.

A Set With Two Elements

Let's add another element to our example set:

{apple, banana}

How many subsets does the set {apple, banana} have?

It could have {apple}, or {banana}, and don't forget:

So a set with two elements has 4 subsets.

A Set With Three Elements

How about:

{apple, banana, cherry}

OK, let's be more systematic now, and list the subsets by how many elements they have:

Subsets with one element: {apple}, {banana}, {cherry}

Subsets with two elements: {apple, banana}, {apple, cherry}, {banana, cherry}

And:

In fact we could put it in a table:

  List Number of
subsets
zero elements {} 1
one element {apple}, {banana}, {cherry} 3
two elements {apple, banana}, {apple, cherry}, {banana, cherry} 3
three elements {apple, banana, cherry} 1
Total: 8

(Note: did you see a pattern in the numbers there?)

Sets with Four Elements (Your Turn!)

Now try to do the same for this set:

{apple, banana, cherry, date}

Here is a table for you:

  List Number of
subsets
zero elements {}  
one element    
two elements    
three elements    
four elements    
Total:  

(Note: if you did this right, there will be a pattern to the numbers.)

 

Sets with Five Elements

And now:

{apple, banana, cherry, date, egg}

Here is a table for you:

  List Number of
subsets
zero elements {}  
one element    
two elements    
three elements    
four elements    
five elements    
Total:  

(Was there a pattern to the numbers?)

 

Sets with Six Elements

What about:

{apple, banana, cherry, date, egg, fudge}

OK ... we don't need to complete a table, because...

... you should be able to see a pattern by now!

Doubling

The first thing to notice is that the total number of subsets doubles each time:

A set with n elements has 2n subsets

So you should be able to answer:

Another Pattern

Now let's think about subsets and sizes:

Do you recognize this pattern of numbers?

They are the numbers from Pascal's Triangle!

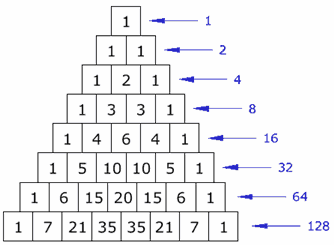
pascals triangle

This is very useful, because now you can check if you have the right number of subsets.

Note: the rows start at 0, and likewise the columns.

Example: For the set {apple, banana, cherry, date, egg} you list subsets of length three:

  • {apple, banana, cherry}
  • {apple, banana, date}
  • {apple, banana, egg}
  • {apple, cherry, egg}

But that is only 4 subsets, how many should there be?

Well, you are choosing 3 out of 5, so go to row 5, position 3 of Pascal's Triangle (remember to start counting at 0) to find you need 10 subsets, so you must think harder!

In fact these are the results: {apple,banana,cherry} {apple,banana,date} {apple,banana,egg} {apple,cherry,date} {apple,cherry,egg} {apple,date,egg} {banana,cherry,date} {banana,cherry,egg} {banana,date,egg} {cherry,date,egg}

Calculating The Numbers

Is there a way of calculating the numbers such as 1, 4, 6, 4 and 1 (instead of looking them up in Pascal's Triangle)?

Yes, we can find the number of ways of selecting each number of elements using Combinations.

There are four elements in the set, and:

  • The number of ways of selecting 0 elements from 4 = 4C0 = 1
  • The number of ways of selecting 1 element from 4  = 4C1 = 4
  • The number of ways of selecting 2 elements from 4 = 4C2 = 6
  • The number of ways of selecting 3 elements from 4 = 4C3 = 4
  • The number of ways of selecting 4 elements from 4 = 4C4 = 1
  •                                                  Total number of subsets = 16

 

Can you do the same for a set with five elements?

Complete the following:

  • The number of ways of selecting 0 elements from 5 = 5C0 = 1
  • The number of ways of selecting 1 element from 5  = ___________
  • The number of ways of selecting 2 elements from 5 = ___________
  • The number of ways of selecting 3 elements from 5 = ___________
  • The number of ways of selecting 4 elements from 5 = ___________ 
  • The number of ways of selecting 5 elements from 5 = ___________
  •                                         Total number of subsets = ___________

Conclusion

In this activity you have:

More importantly you have learned how different branches of mathematics can be combined together.

 

Introduction to Sets Activity Index