Exponential Growth and Decay
Exponential growth can be amazing!
 |
Let us say we have this special tree. It grows exponentially, following this formula: Height (in mm) = ex
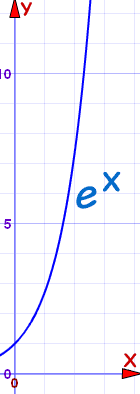
No tree could ever grow that tall! So when people say "it grows exponentially" ... just think what that means. |
Growth and Decay
But sometimes things can grow (or the opposite: decay) exponentially, at least for a while.
So we have a generally useful formula:
y(t) = a × ekt
Where y(t) = value at time "t"
a = value at the start
k = rate of growth (when >0) or decay (when <0)
t = time
Example: 2 months ago you had 3 mice, you now have 18.
 |
Assuming the growth continues like that
|
Start with the formula:
y(t) = a × ekt
We know a=3 mice, t=2 months, and right now y(2)=18 mice:
18 = 3 × e2k
Now some algebra to solve for k:
| Divide both sides by 3: | 6 = e2k | |
| Take the natural logarithm of both sides: | ln(6) = ln(e2k) | |
| ln(ex)=x, so: | ln(6) = 2k | |
| Rearrange: | k = ln(6)/2 |
Now, we want to know the population in 2 more months (at t=4 months), and in 1 year from now (t=14 months):
y(4) = 3 e(ln(6)/2)×4 = 108
y(14) = 3 e(ln(6)/2)×14 = 839,808
That's a lot of mice! I hope you will be feeding them properly.
Exponential Decay
Some things "decay" (get smaller) exponentially.
Example: Atmospheric pressure (the pressure of air around you) decreases as you go higher.
It decreases about 12% for every 1000 m: an exponential decay.
The pressure at sea level is about 1013 hPa (depending on weather).
- Write the formula (with its "k" value),
- What would the pressure be on the roof of the Empire State Building (381 m),
- and at the top of Mount Everest (8848 m)?
Start with the formula:
y(t) = a × ekt
We know
- a (the pressure at sea level) = 1013 hPa
- t is in meters (distance, not time, but the formula still works)
- y(1000) is a 12% reduction on 1013 hPa = 891.44 hPa
So:
891.44 = 1013 ek×1000
Now some algebra to solve for k:
| Divide both sides by 1013: | 0.88 = e1000k | |
| Take the natural logarithm of both sides: | ln(0.88) = ln(e1000k) | |
| ln(ex)=x, so: | ln(0.88) = 1000k | |
| Rearrange: | k = ln(0.88)/1000 |
Now we know "k" we can write:
y(t) = 1013 e(ln(0.88)/1000)×t
And finally we can calculate the pressure at 381 m, and at 8848 m:
y(381) = 1013 e(ln(0.88)/1000)×381 = 965 hPa
y(8848) = 1013 e(ln(0.88)/1000)×8848 = 327 hPa
(In fact pressures at Mount Everest are around 337 hPa ... not bad!)