Solving Inequality Word Questions

(You might like to read Introduction to Inequalities and Solving Inequalities first.)


In Algebra we have "inequality" questions like:

soccer teams

Sam and Alex play in the same soccer team.
Last Saturday Alex scored 3 more goals than Sam, but together they scored less than 9 goals.

What are the possible number of goals Alex scored?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

We should also write down what is actually being asked for, so we know where we are going and when we have arrived!

 

The best way to learn this is by example, so let's try our first example:

soccer teams

Sam and Alex play in the same soccer team.
Last Saturday Alex scored 3 more goals than Sam, but together they scored less than 9 goals.

What are the possible number of goals Alex scored?

 

Assign Letters:

  • the number of goals Alex scored: A
  • the number of goals Sam scored: S

We know that Alex scored 3 more goals than Sam did, so: A = S + 3

And we know that together they scored less than 9 goals: S + A < 9

We are being asked for how many goals Alex might have scored: A

 

Solve:

Start with:S + A < 9
A = S + 3, so:S + (S + 3) < 9
Simplify:2S + 3 < 9
Subtract 3 from both sides:2S < 9 − 3
Simplify:2S < 6
Divide both sides by 2:S < 3

Sam scored less than 3 goals, which means that Sam could have scored 0, 1 or 2 goals.

Alex scored 3 more goals than Sam did, so Alex could have scored 3, 4, or 5 goals.

 

Check:

  • When S = 0, then A = 3 and S + A = 3, and 3 < 9 is correct
  • When S = 1, then A = 4 and S + A = 5, and 5 < 9 is correct
  • When S = 2, then A = 5 and S + A = 7, and 7 < 9 is correct
  • (But when S = 3, then A = 6 and S + A = 9, and 9 < 9 is incorrect)

Lots More Examples!

pups

Example: Of 8 pups, there are more girls than boys.

How many girl pups could there be?

Assign Letters:

  • the number of girls: g
  • the number of boys: b

We know that there are 8 pups, so: g + b = 8, which can be rearranged to

b = 8 − g

We also know there are more girls than boys, so:

g > b

We are being asked for the number of girl pups: g

Solve:

Start with:g > b
b = 8 − g, so:g > 8 − g
Add g to both sides:g + g > 8
Simplify:2g > 8
Divide both sides by 2:g > 4

So there could be 5, 6, 7 or 8 girl pups.

Could there be 8 girl pups? Then there would be no boys at all, and the question isn't clear on that point (sometimes questions are like that).

Check

  • When g = 8, then b = 0 and g > b is correct (but is b = 0 allowed?)
  • When g = 7, then b = 1 and g > b is correct
  • When g = 6, then b = 2 and g > b is correct
  • When g = 5, then b = 3 and g > b is correct
  • (But if g = 4, then b = 4 and g > b is incorrect)

A speedy example:

bike

Example: Joe enters a race where he has to cycle and run.

He cycles a distance of 25 km, and then runs for 20 km. His average running speed is half of his average cycling speed.

Joe completes the race in less than 2½ hours, what can we say about his average speeds?

Assign Letters:

  • Average running speed: s
  • So average cycling speed: 2s

Formulas:

  • Speed = DistanceTime
  • Which can be rearranged to: Time = DistanceSpeed

We are being asked for his average speeds: s and 2s

 

The race is divided into two parts:

1. Cycling

  • Distance = 25 km
  • Average speed = 2s km/h
  • So Time = DistanceAverage Speed = 252s hours

2. Running

  • Distance = 20 km
  • Average speed = s km/h
  • So Time = DistanceAverage Speed = 20s hours

Joe completes the race in less than 2½ hours

  • The total time < 2½
  • 252s + 20s < 2½

Solve:

Start with:252s + 20s < 2½
Multiply all terms by 2s:25 + 40 < 5s
Simplify:65 < 5s
Divide both sides by 5:13 < s
Swap sides:s > 13

So his average speed running is greater than 13 km/h and his average speed cycling is greater than 26 km/h

In this example we get to use two inequalities at once:

ball throw

Example: The velocity v m/s of a ball thrown directly up in the air is given by v = 20 − 10t, where t is the time in seconds.

At what times will the velocity be between 10 m/s and 15 m/s?

Letters:

  • velocity in m/s: v
  • the time in seconds: t

Formula:

  • v = 20 − 10t

We are being asked for the time t when v is between 5 and 15 m/s:

10  <  v  <  15
10  <  20 − 10t  <  15

Solve:

Start with:
10  <  20 − 10t  <  15
Subtract 20 from each:
10− 20  <  20 − 10t− 20  <  15− 20
Simplify:
−10  < −10t  <  −5
Divide each by 10:
−1  < −t  <  −0.5
Change signs and reverse inequalities:
1  >  t  >  0.5
It is neater to show the smaller
number first, so swap over:
0.5  <  t  <  1

So the velocity is between 10 m/s and 15 m/s between 0.5 and 1 second after.

And a reasonably hard example to finish with:

Example: A rectangular room fits at least 7 tables that each have 1 square meter of surface area. The perimeter of the room is 16 m.
What could the width and length of the room be?

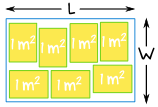
room size

Make a sketch: we don't know the size of the tables, only their area, they may fit perfectly or not!

Assign Letters:

  • the length of the room: L
  • the width of the room: W

The formula for the perimeter is 2(W + L), and we know it is 16 m

  • 2(W + L) = 16
  • W + L = 8
  • L = 8 − W

We also know the area of a rectangle is the width times the length: Area = W × L

And the area must be greater than or equal to 7:

  • W × L ≥ 7

We are being asked for the possible values of W and L

 

Let's solve:

Start with:
W × L ≥ 7
Substitute L = 8 − W:
W × (8 − W) ≥ 7
Expand:
8W − W2 ≥ 7
Bring all terms to left hand side:
W2 − 8W + 7 ≤ 0
This is a quadratic inequality. It can be solved many way, here we will solve it by completing the square:
Move the −7 to the right side of the inequality:
W2 − 8W ≤ −7
Complete the square on the left side of the inequality and balance this by adding the same value to the right side of the inequality:
W2 − 8W + 16 ≤ −7 + 16
Simplify:
(W − 4)2 ≤ 9
Square root on both sides of the inequality:
−3 ≤ W − 4 ≤ 3
Yes we have two inequalities, because 32 = 9 AND (−3)2 = 9
Add 4 to both sides of each inequality:
1 ≤ W ≤ 7

So the width must be between 1 m and 7 m (inclusive) and the length is 8−width.

 

Check:

  • Say W = 1, then L = 8−1 = 7, and A = 1 x 7 = 7 m2 (fits exactly 7 tables)
  • Say W = 0.9 (less than 1), then L = 7.1, and A = 0.9 x 7.1 = 6.39 m2 (7 won't fit)
  • Say W = 1.1 (just above 1), then L = 6.9, and A = 1.1 x 6.9 = 7.59 m2 (7 fit easily)
  • Likewise for W around 7 m

 

5550, 5551, 5552, 5553, 7083, 9376, 9377, 9378, 2727, 7182
Inequalities Solving Inequalities Graphing Linear Inequalities Inequality Grapher Algebra Index