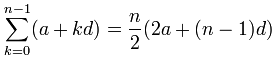Arithmetic Sequences and Sums
Sequence
A sequence is a set of things (usually numbers) that are in order.
Each number in a sequence is called a term (or sometimes "element" or "member"), read Sequences and Series for more details.
Arithmetic Sequence
In an arithmetic sequence the difference between one term and the next is a constant.
In other words, we add the same value each time ... infinitely.
Example: 1, 4, 7, 10, 13, 16, 19, 22, 25, ...
This sequence has a difference of 3 between each number.
We continue the pattern by adding 3 each time, like this:
In general we can write an arithmetic sequence like this:
{a, a+d, a+2d, a+3d, ... }
where:
- a is the first term, and
- d is the difference between the terms (called the "common difference")
Example (continued): 1, 4, 7, 10, 13, 16, 19, 22, 25, ...
Has:
- a = 1 (the first term)
- d = 3 (the common difference between terms)
And we get:
{a, a+d, a+2d, a+3d, ... }
{1, 1+3, 1+2×3, 1+3×3, ... }
{1, 4, 7, 10, ... }
Rule
We can write an arithmetic sequence as a rule:
xn = a + d(n−1)
(We use "n−1" because d is not used in the 1st term).
Example: find a rule, and calculate the 9th term, for this arithmetic sequence:
3, 8, 13, 18, 23, 28, 33, 38, ...
The common difference is 5.
The values of a and d are:
- a = 3 (the first term)
- d = 5 (the common difference)
Using the arithmetic sequence rule:
So the 9th term is:
x9 = 5×9 − 2
= 43
Is that right? Check for yourself!
Arithmetic sequences are sometimes called arithmetic progressions (A.P.’s)
Advanced Topic: Summing an Arithmetic Series
To sum up the terms of this arithmetic sequence:
a + (a+d) + (a+2d) + (a+3d) + ...
use this formula:
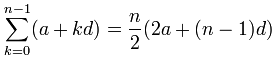
What is that funny symbol? It is called Sigma Notation
And below and above it are shown the starting and ending values:
It says "Sum up n where n goes from 1 to 4". Answer=10
Here is how to use it:
Example: Add the first 10 terms of this sequence:
{ 1, 4, 7, 10, 13, ... }
The values of a, d and n are:
- a = 1 (the first term)
- d = 3 (the common difference)
- n = 10 (how many terms to add up)
So:
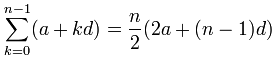
Becomes:
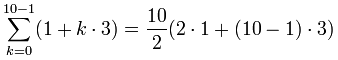
= 5(2+9·3) = 5(29) = 145
Check: why don't you add up the terms yourself, and see if it comes to 145
Footnote: Why Does the Formula Work?
Let’s see the cleverness behind the formula.
First, we will call the whole sum "S":
Next, rewrite S in reverse order:
Now add those two, term by term:
| S | = | a | + | (a+d) | + | ... | + | (a + (n-2)d) | + | (a + (n-1)d) |
| S | = | (a + (n-1)d) | + | (a + (n-2)d) | + | ... | + | (a + d) | + | a |
| 2S | = | (2a + (n-1)d) | + | (2a + (n-1)d) | + | ... | + | (2a + (n-1)d) | + | (2a + (n-1)d) |
Each term is the same! And there are "n" of them so ...
Now, just divide by 2 and we get:
S = n2 (2a + (n−1)d)
Which is our formula: