Systems of Linear and Quadratic Equations

	A Linear Equation is an equation of a line.
	A Quadratic Equation is the equation of a parabola and has at least one variable squared (such as x²)
	And together they form a System of a Linear and a Quadratic Equation

A System of those two equations can be solved (find where they intersect), either:

Graphically (by plotting them both on the Function Grapher and zooming in)
or using Algebra

How to Solve using Algebra

Make both equations into "y =" format
Set them equal to each other
Simplify into "= 0" format (like a standard Quadratic Equation)
Solve the Quadratic Equation!
Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers

An example will help:

Example: Solve these two equations:

y = x² - 5x + 7
y = 2x + 1

Make both equations into "y=" format:

They are both in "y=" format, so go straight to next step

Set them equal to each other

x² - 5x + 7 = 2x + 1

Simplify into "= 0" format (like a standard Quadratic Equation)

Subtract 2x from both sides: x² - 7x + 7 = 1

Subtract 1 from both sides: x² - 7x + 6 = 0

Solve the Quadratic Equation!

(The hardest part for me)

You can read how to solve Quadratic Equations, but here we will factor the Quadratic Equation:

Start with: x² - 7x + 6 = 0

Rewrite -7x as -x-6x: x² - x - 6x + 6 = 0

Then: x(x-1) - 6(x-1) = 0

Then: (x-1)(x-6) = 0

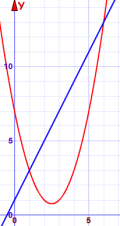
linear and quadratic

Which gives us the solutions x=1 and x=6

Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers

The matching y values are (also see Graph):

for x=1: y = 2x+1 = 3
for x=6: y = 2x+1 = 13

Our solution: the two points are (1,3) and (6,13)

I think of it as three stages:

Combine into Quadratic Equation ⇒ Solve the Quadratic ⇒ Calculate the points

Solutions

There are three possible cases:

No real solution (happens when they never intersect)
One real solution (when the straight line just touches the quadratic)
Two real solutions (like the example above)

linear and quadratic different intersections

Time for another example!

Example: Solve these two equations:

y - x² = 7 - 5x
4y - 8x = -21

Make both equations into "y=" format:

First equation is: y - x² = 7 - 5x

Add x² to both sides: y = x² + 7 - 5x

Second equation is: 4y - 8x = -21

Add 8x to both sides: 4y = 8x - 21

Divide all by 4: y = 2x - 5.25

Set them equal to each other

x² - 5x + 7 = 2x - 5.25

Simplify into "= 0" format (like a standard Quadratic Equation)

Subtract 2x from both sides: x² - 7x + 7 = -5.25

Add 5.25 to both sides: x² - 7x + 12.25 = 0

Solve the Quadratic Equation!

Using the Quadratic Formula from Quadratic Equations:

linear and quadratic one intersection

x = [ -b ± √(b²-4ac) ] / 2a
x = [ 7 ± √((-7)²-4×1×12.25) ] / 2×1
x = [ 7 ± √(49-49) ] / 2
x = [ 7 ± √0 ] / 2
x = 3.5

Just one solution! (The "discriminant" is 0)

Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers

The matching y value is:

for x=3.5: y = 2x-5.25 = 1.75

Our solution: (3.5,1.75)

Real World Example

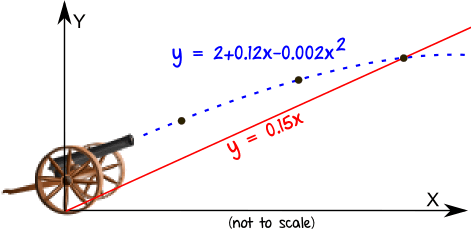
Kaboom!

The cannon ball flies through the air, following a parabola:

y = 2 + 0.12x - 0.002x²

The land slopes upward: y = 0.15x

Where does the cannon ball land?

linear quadratic cannon shot

Both equations are already in the "y =" format, so set them equal to each other:

0.15x = 2 + 0.12x - 0.002x²

Simplify into "= 0" format:

Bring all terms to left: 0.002x² + 0.15x - 0.12x - 2 = 0

Simplify: 0.002x² + 0.03x - 2 = 0

Multiply by 500: x² + 15x - 1000 = 0

Solve the Quadratic Equation:

Split 15x into -25x+40x: x² -25x + 40x - 1000 = 0

Then: x(x-25) + 40(x-25) = 0

Then: (x+40)(x-25) = 0

x = -40 or 25

The negative answer can be ignored, so x = 25

Use the linear equation to calculate matching "y" value:

y = 0.15 x 25 = 3.75

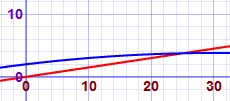
So the cannonball impacts the slope at (25, 3.75)

You can also find the answer graphically by using the Function Grapher:

linear quadratic graph

Both Variables Squared

Sometimes BOTH terms of the quadratic can be squared:

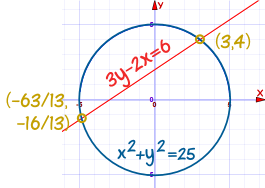
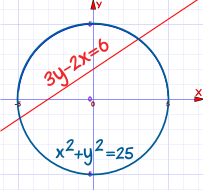
Example: Find the points of intersection of

The circle x² + y² = 25

And the straight line 3y - 2x = 6

line 3y-2x=6 vs circle x^2+y^2=25

First put the line in "y=" format:

Move 2x to right hand side: 3y = 2x + 6

Divide by 3: y = 2x/3 + 2

NOW, Instead of making the circle into "y=" format, we can use substitution (replace "y" in the quadratic with the linear expression):

Put y = 2x/3 + 2 into circle equation: x² + (2x/3 + 2)² = 25

Expand: x² + 4x²/9 + 2(2x/3)(2) + 2² = 25

Multiply all by 9: 9x² + 4x² + 2(2x)(2)(3) + (9)(2²) = (9)(25)

Simplify: 13x²+ 24x + 36 = 225

Subtract 225 from both sides: 13x²+ 24x - 189 = 0

Now it is in standard Quadratic form, let's solve it:

13x²+ 24x - 189 = 0

Split 24x into 63x-39x: 13x²+ 63x - 39x - 189 = 0

Then: x(13x + 63) - 3(13x + 63) = 0

Then: (x - 3)(13x + 63) = 0

So: x = 3 or -63/13

Now work out y-values:

Substitute x = 3 into linear equation:

3y - 6 = 6
3y = 12
y = 4
So one point is (3, 4)

Substitute x = -63/13 into linear equation:

3y + 126/13 = 6
y + 42/13 = 2
y = 2 - 42/13 = 26/13 - 42/13 = -16/13
So the other point is (-63/13, -16/13)

line 3y-2x=6 vs circle x^2+y^2=25

8184, 8185, 8186, 8187, 8188, 8189, 8190, 8191, 8192, 8193, 8194, 8195, 8196, 8197, 8198