Theorems, Corollaries, Lemmas

What are all those things? They sound so impressive!

Well, they are basically just facts: some result that has been arrived at.

A Theorem is a major result
A Corollary is a theorem that follows on from another theorem
A Lemma is a small result (less important than a theorem)

Examples

Here is an example from Geometry:

Example: A Theorem and a Corollary

Theorem:

Angles on one side of a straight line always add to 180°.

angles add to 180 degrees

Corollary:

Following on from that theorem we find that where two lines intersect, the angles opposite each other (called Vertical Angles) are equal (a=c and b=d in the diagram).

vertically-opposite-abcd
Angle a = angle c
Angle b = angle d

Proof:

Angles a and b add to 180° because they are along a line:

a + b = 180°

a = 180° − b

Likewise for angles b and c

b + c = 180°

c = 180° − b

And since both a and c equal 180° − b, then

a = c

And a slightly more complicated example from Geometry:

Example: A Theorem, a Corollary to it, and also a Lemma!

Theorem:

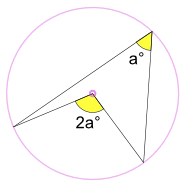
inscribed angle 2a and a
An inscribed angle a° is half of the central angle 2a°
Called the Angle at the Center Theorem.

Proof: Join the center O to A.

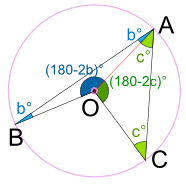
inscribed angle proof

Triangle ABO is isosceles (two equal sides, two equal angles), so:

Angle OBA = Angle BAO = b°

And, using Angles of a Triangle add to 180°:

Angle AOB = (180 − 2b)°

Triangle ACO is isosceles, so:

Angle OCA = Angle CAO = c°

And, using Angles of a Triangle add to 180°:

Angle AOC = (180 − 2c)°

And, using Angles around a point add to 360°:

Angle BOC = 360° − (180 − 2b)° − (180 − 2c)°

= 2b° + 2c°

= 2(b + c)°

Replace b + c with a, we get:

Angle BAC = a° and Angle BOC = 2a°

inscribed angle 2a and a

And we have proved the theorem.

(That was a "major" result, so is a Theorem.)

Corollary

(This is called the "Angles Subtended by the Same Arc Theorem", but it’s really just a Corollary of the "Angle at the Center Theorem")

Keeping the endpoints fixed ... ... the angle a° is always the same, no matter where it is on the circumference:

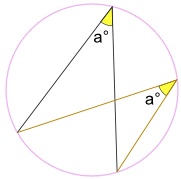
inscribed angle a and a

So, Angles Subtended by the Same Arc are equal.

Lemma

(This is sometimes called the "Angle in the Semicircle Theorem", but it’s really just a Lemma to the "Angle at the Center Theorem")

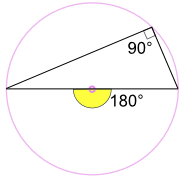
inscribed angle 2a and a angle semicircle 180 and 90

In the special case where the central angle forms a diameter of the circle:

2a° = 180° , so a° = 90°

So an angle inscribed in a semicircle is always a right angle.

(That was a "small" result, so it is a Lemma.)

Another example, related to Pythagoras' Theorem:

Example:

Theorem

If m and n are any two whole numbers and

a = m² − n²
b = 2mn
c = m² + n²

then a² + b² = c²

Proof:

a² + b² = (m² − n²)² + (2mn)²

= m⁴ − 2m²n² + n⁴ + 4m²n²

= m⁴ + 2m²n² + n⁴

= (m² + n²)²

= c²

(That was a "major" result.)

Corollary

a, b and c, as defined above, are a Pythagorean Triple

Proof:

From the Theorem a² + b² = c²,
so a, b and c are a Pythagorean Triple

(That result "followed on" from the previous Theorem.)

Lemma

If m = 2 and n = 1, then we get the Pythagorean triple 3, 4 and 5

Proof:

If m = 2 and n = 1, then

a = 2² − 1² = 4 − 1 = 3
b = 2 × 2 × 1 = 4
c = 2² + 1² = 4 + 1 = 5

(That was a "small" result.)