Solving AAS Triangles

"AAS" means "Angle, Angle, Side"

"AAS" is when we know two angles and one side (which is not between the angles).

To solve an AAS triangle

trig AAS example

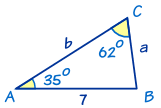
In this triangle we know:

We can first find angle B by using 'angles of a triangle add to 180°':

B = 180° − 35° − 62° = 83°

To find side a we can use The Law of Sines:

a/sin(A) = c/sin(C)

a/sin(35°) = 7/sin(62°)

Multiply both sides by sin(35°):

a = sin(35°) × 7/sin(62°)
a = 4.55 to 2 decimal places

To find side b we can also use The Law of Sines:

b/sin(B) = c/sin(C)

b/sin(83°) = 7/sin(62°)

Multiply both sides by sin(83°):

b = sin(83°) × 7/sin(62°)
b = 7.87 to 2 decimal places

Now we have completely solved the triangle!

We used b/sin(B) = c/sin(C) rather than b/sin(B) = a/sin(A) for the last calculation ... why?

There's a good reason for that. What if we made a mistake when finding a? Then our answer for b would also be wrong!

As a rule, it is always better to use the sides and angles that are given rather than ones we've just worked out.

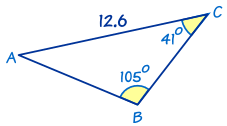
trig AAS example

This is also an AAS triangle.

First find angle A by using "angles of a triangle add to 180°":

A = 180° − 41° − 105° = 34°

Now find side c by using The Law of Sines:

c/sin(C) = b/sin(B)

c/sin(41°) = 12.6/sin(105°)

c = sin(41°) × 12.6/sin(105°)

c = 8.56 to 2 decimal places

Similarly we can find side a by using The Law of Sines and using the given side b = 12.6 (rather than side c that we just worked out):

a/sin(A) = b/sin(B)

a/sin(34°) = 12.6/sin(105°)

a = sin(34°) × 12.6/sin(105°)

a = 7.29 to 2 decimal places

Done!

261, 3956, 1540, 262, 1541, 1542, 1560, 2370, 2371, 3955