Solving SSA Triangles

"SSA" means "Side, Side, Angle"

Triangle with two sides and a non-included angle labeled

"SSA" is when we know two sides and an angle that's not the angle between the sides.

To solve an SSA triangle

Example 1

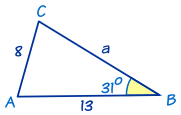
Triangle with angle B=31 degrees, side b=8, and side c=13

In this triangle we know

  • angle B = 31°
  • b = 8
  • and c = 13

In this case, we can use The Law of Sines first to find angle C:

sin(C)/c = sin(B)/b
sin(C)/13 = sin(31°)/8
sin(C) = (13×sin(31°))/8
sin(C) = 0.8369...
C = sin−1(0.8369...)
C = 56.818...°   (* but see below)
C = 56.8° to one decimal place

Next, we can use the three angles add to 180° to find angle A:

A = 180° − 31° − 56.818...°
A = 92.181...° = 92.2° to one decimal place

Now we can use The Law of Sines again to find a:

a/sin(A) = b/sin(B)
a/sin(92.181...°) = 8/sin(31°)

Notice that we didn't use A = 92.2°, that angle is rounded to 1 decimal place. It is much better to use the unrounded number 92.181...° which should still be on our calculator from the last calculation.

a = (sin(92.181...°) × 8)/sin(31°)
a = 15.52 to 2 decimal places

So, we have completely solved the triangle ...

... or have we?

* Back when we calculated:

C = sin−1(0.8369...)
C = 56.818...°

We didn't include that sin−1(0.8369...) might have two answers (see Law of Sines):

The other answer for C is 180° − 56.818...°

Here you can see why we have two possible answers:

Arc showing side b swinging to two possible intersection points on the base

By swinging side "8" left and right we can
join up with side "a" in two possible locations.

This is called the Ambiguous Case.

So let's go back and continue our example:

The other possible angle is:

C = 180° − 56.818...°
C = 123.2° to one decimal place

With a new value for C we'll have new values for angle A and side a

Use "the three angles add to 180°" to find angle A:

A = 180° − 31° − 123.181...°
A = 25.818...°
A = 25.8° to one decimal place

Now we can use The Law of Sines again to find a:

a/sin(A) = b/sin(B)
a/sin(25.818...°) = 8/sin(31°)
a = (sin(25.818...°)×8)/sin(31°)
a = 6.76 to 2 decimal places

So the two sets of answers are:

C = 56.8°, A = 92.2°, a = 15.52

C = 123.2°, A = 25.8°, a = 6.76

Example 2

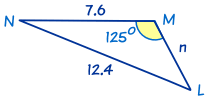
Obtuse triangle with angle M=125 degrees, side m=12.4, and side l=7.6

This is also an SSA triangle.

In this triangle we know angle M = 125°, m = 12.4 and l = 7.6

We'll use The Law of Sines to find angle L first:

sin(L)/l = sin(M)/m
sin(L)/7.6 = sin(125°)/12.4
sin(L) = (7.6×sin(125°))/12.4
sin(L) = 0.5020...
L = 30.136...°
L = 30.1° to one decimal place

Next, we'll use "the three angles add to 180°" to find angle N:

N = 180° − 125° − 30.136...°
N = 24.863...°
N = 24.9° to one decimal place

Now we'll use The Law of Sines again to find n:

n/sin(N) = m/sin(M)
n/sin(24.863...°) = 12.4/sin(125°)
n = (sin(24.863...°)×12.4)/sin(125°)
n = 6.36 to 2 decimal places
trig SSA example

Note there's only one answer in this case. The "12.4" line only joins up one place.

The other possible answer for L is 149.9°. But that's impossible because we already have M = 125° and a triangle can't have two angles greater than 90°.

Example 3: What the ... ?

  • angle A = 35°
  • side a = 4
  • side c = 9
sin(C)9 = sin(35°)4
sin(C) = 9 × sin(35°)4
sin(C) = 1.29...

Wait! The sine of an angle can never be greater than 1. This means no such triangle exists.

Conclusion:

When solving a "Side, Side, Angle" triangle we start with the Law of Sines, but need to check if there's zero, one or two possible answers!

267, 3960, 1529, 1549, 268, 1550, 1563, 2376, 2377, 3959
Triangle Solving Practice The Law of Sines The Law of Cosines Solving Triangles Trigonometry Index Algebra Index