Cross Product

A vector has magnitude (how long it is) and direction:

Two vectors can be multiplied using the "Cross Product" (also see Dot Product)

The Cross Product a × b of two vectors is another vector that is at right angles to both:

And it all happens in 3 dimensions!

The magnitude (length) of the cross product equals the area of a parallelogram with vectors a and b for sides:

See how it changes for different angles:

The cross product (blue) is:

• zero in length when vectors a and b point in the same, or opposite, direction
• reaches maximum length when vectors a and b are at right angles

And it can point one way or the other!

So how do we calculate it?

Calculating

We can calculate the Cross Product this way:

a × b = |a| |b| sin(θ) n

• |a| is the magnitude (length) of vector a
• |b| is the magnitude (length) of vector b
• θ is the angle between a and b
• n is the unit vector at right angles to both a and b

So the length is: the length of a times the length of b times the sine of the angle between a and b,

Then we multiply by the vector n so it heads in the correct direction (at right angles to both a and b).

OR we can calculate it this way:

When a and b start at the origin point (0,0,0), the Cross Product will end at:

• c_x = a_yb_z − a_zb_y
• c_y = a_zb_x − a_xb_z
• c_z = a_xb_y − a_yb_x

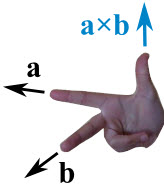
Which Direction?

The cross product could point in the completely opposite direction and still be at right angles to the two other vectors, so we have the:

"Right Hand Rule"

With your right-hand, point your index finger along vector a, and point your middle finger along vector b: the cross product goes in the direction of your thumb.

Dot Product

The Cross Product gives a vector answer, and is sometimes called the vector product.

But there is also the Dot Product which gives a scalar (ordinary number) answer, and is sometimes called the scalar product.

Question: What do you get when you cross an elephant with a banana?

Answer: |elephant| |banana| sin(θ) n