Standard Deviation and Variance
Deviation means how far from the normal
Standard Deviation
The Standard Deviation is a measure of how spread out numbers are.
Its symbol is σ (the greek letter sigma)
The formula is easy: it is the square root of the Variance. So now you ask, "What's the Variance?"
Variance
The Variance is defined as:
The average of the squared differences from the Mean.
To calculate the variance follow these steps:
- Calculate the Mean (the simple average of the numbers)
- Then for each number: subtract the Mean and square the result (the squared difference)
- Then calculate the average of those squared differences. (Why Square?)
Example
You and your friends have just measured the heights of your dogs (in millimeters):
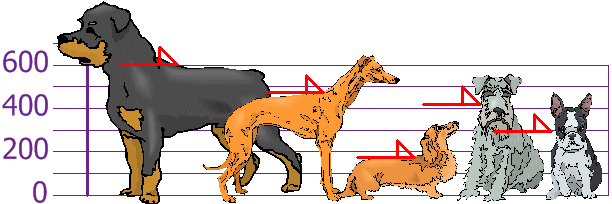
The heights (at the shoulders) are: 600 mm, 470 mm, 170 mm, 430 mm and 300 mm.
Discover the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:
Answer:
| Mean | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
so the mean (average) height is 394 mm. Let's plot this on the chart:
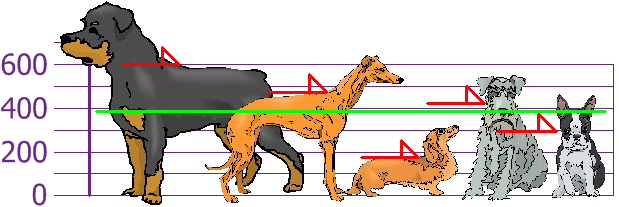
Now we calculate each dog's difference from the Mean:
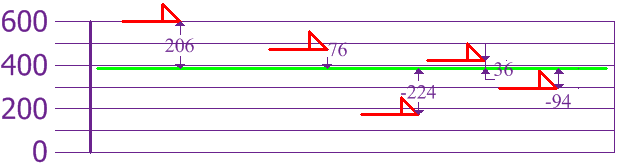
To calculate the Variance, take each difference, square it, and then average the result:
| Variance | ||
| σ2 | = | 2062 + 762 + (−224)2 + 362 + (−94)25 |
| = | 42436 + 5776 + 50176 + 1296 + 88365 | |
| = | 1085205 | |
| = | 21704 | |
So the Variance is 21,704
And the Standard Deviation is just the square root of Variance, so:
| Standard Deviation | ||
| σ | = | √21704 |
| = | 147.32... | |
| = | 147 (to the nearest mm) | |
Note: Variance uses squared units. Here it is 21,704 mm2. Taking the square root gives Standard Deviation back in millimeters.
The good thing about the Standard Deviation is that it is useful. Now we can show which heights are within one Standard Deviation (147 mm) of the Mean:
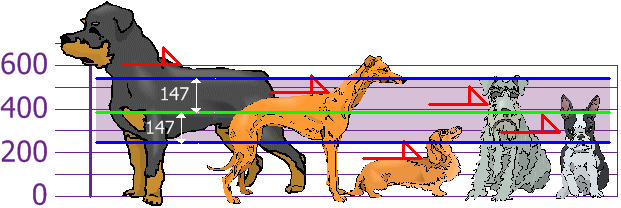
So, using the Standard Deviation we have a "standard" way of knowing what's normal, and what's extra large or extra small.
Rottweilers are tall dogs. And Dachshunds are a bit short, right?
Why is it Useful?
When the data is bell-shaped (normal):
- about 68% of values are within 1 standard deviation of the mean
- and about 95% of values are within 2 standard deviations
So it gives a really good idea of what values to expect.
But with skewed data or outliers, these percentages may be very different.
Read Standard Normal Distribution to learn more.
Also try the Standard Deviation Calculator.
But ... there's a small change for Sample Data
Our example has been for a Population (the 5 dogs are the only dogs we are interested in).
But if the data is a Sample (a selection taken from a bigger Population), then the calculation changes!
When we have N data values that are:
- The Population: divide by N when calculating Variance (like we did)
- A Sample: divide by N−1 when calculating Variance
All other calculations stay the same, including how we calculated the mean.
Example: if our 5 dogs are just a sample from a bigger population of dogs, we divide by 4 instead of 5 like this:
Dividing by N−1 instead of N is called Bessel's correction: it gives a slightly larger variance because a small sample may not show all the variation in the population.
Standard Deviation Recipe
- Find the mean
- Find each difference from the mean
- Square each difference
- Average the squares: divide by N (population) or N-1 (sample)
- Take the square root
Formulas
Here are the two formulas, explained at Standard Deviation Formulas if you want to know more:
|
The "Population Standard Deviation": |
||
| The "Sample Standard Deviation": |
Looks complicated, but the important change is to
divide by N−1 (instead of N) when calculating a Sample Standard Deviation.
*Footnote: Why square the differences?
If we just add up the differences from the mean ... the negatives cancel the positives:
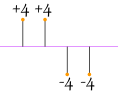 |
4 + 4 − 4 − 44 = 0 |
So that won't work. How about we use absolute values?
 |
|4| + |4| + |−4| + |−4|4 = 4 + 4 + 4 + 44 = 4 |
That looks good (and is the Mean Deviation), but what about this case:
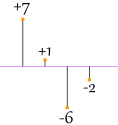 |
|7| + |1| + |−6| + |−2|4 = 7 + 1 + 6 + 24 = 4 |
Oh No! It also gives a value of 4, Even though the differences are more spread out.
So let's try squaring each difference (and taking the square root at the end):
 |
√(42 + 42 + (-4)2 + (-4)24) = √(644) = 4 | |
 |
√(72 + 12 + (-6)2 + (-2)24) = √(904) = 4.74... |
That's nice! The Standard Deviation is bigger when the differences are more spread out ... just what we want.
In fact this method is a similar idea to distance between points, just applied in a different way.
And it is easier to use algebra on squares and square roots than absolute values, which makes the standard deviation easy to use in other areas of mathematics.