Area of Irregular Polygons

Introduction

I just thought I would share with you a clever technique I once used to find the area of general polygons.

The polygon could be regular (all angles are equal and all sides are equal) or irregular

regular irregular
Regular Irregular

The Example Polygon

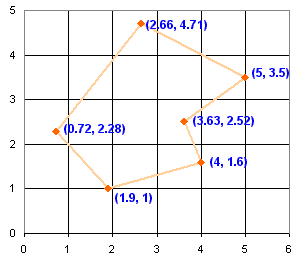
Let's use this polygon as an example:

irregular polygon

Coordinates

The first step is to turn each vertex (corner) into a coordinate, like on a graph:

irregular polygon coords

Area Under One Line Segment

Now, for each line segment, work out the area down to the x-axis.

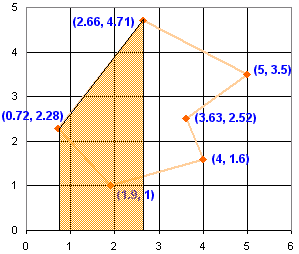
irregular polygon coords and area of one graph trapezoid

So, how do we calculate each area?

area of graph trapezoid is width by average height

Average the two heights, then multiply by the width

Example: For the shape highlighted above, we take the two heights (the "y" coordinates 2.28 and 4.71) and work out the average height:

(2.28+4.71)/2 = 3.495

Work out the width (the difference between the "x" coordinates 2.66 and 0.72)

2.66-0.72 = 1.94

The area is width×height:

1.94 × 3.495 = 6.7803

 

Add Them All Up

Now add them all up!

But the trick is to add when they go forwards (positive width), and subtract when they go backwards (negative width).

If you always go clockwise around the polygon, and always subtract the first "x" coordinate from the second, it works out naturally, like this:

From To      
x y x y Avg Height Width (+/−) Area (+/−)
0.72 2.28 2.66 4.71 3.495 1.94 6.7803
2.66 4.71 5 3.5 4.105 2.34 9.6057
5 3.5 3.63 2.52 3.01 −1.37 −4.1237
3.63 2.52 4 1.6 2.06 0.37 0.7622
4 1.6 1.9 1 1.3 −2.1 −2.7300
1.9 1 0.72 2.28 1.64 −1.18 −1.9352
          Total: 8.3593

You can also go the other direction. If you get a negative area just make it positive.

And it looks like this:

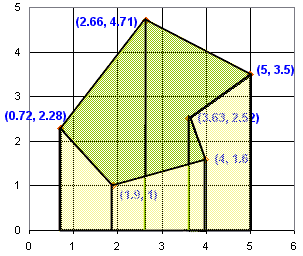
irregular polygon area all trapezoids

So that's it! The area is 8.3593

Area of Polygon Tool

Glad you read this far! You are rewarded with a link to the Area of a Polygon Drawing Tool that can do all of this for you. It also accepts manual entry of coordinates.

Formulas

Let us play with some formulas!

irregular triangle

Let's start with a a simple triangle, with coordinates (x1, y1), (x2, y2), (x3, y3)

Multiplying widths by average heights gets:

Area = (x2−x1)(y1+y2)/2 + (x3−x2)(y2+y3)/2 + (x1−x3)(y3+y1)/2

But we can rewrite it! Let us expand the whole thing so we can do some surgery on it:

2×Area = x2y1 + x2y2 − x1y1 − x1y2 + x3y2 + x3y3 − x2y2 − x2y3 + x1y3 + x1y1 − x3y3 − x3y1

Collect like terms:

2×Area = x2y1 + x2y2−x2y2 + x1y1−x1y1 − x1y2 + x3y2 + x3y3−x3y3 − x2y3 + x1y3  − x3y1

Simplify:

2×Area = x2y1 − x1y2 + x3y2 − x2y3 + x1y3 − x3y1

Rearranging the terms (and changing signs) we get the so-called "shoelace formula":

−2×Area = x1y2 + x2y3 + x3y1 − x2y1 − x3y2 − x1y3

In General

irregular triangle

In general (for an n-sided simple polygon), using absolute values || we have:

Area = ½| (x2−x1)(y1+y2) + (x3−x2)(y2+y3) + ... + (x1−xn)(yn+y1) |

or the Shoelace version:

Area = ½| x1y2 + x2y3 + ... + xny1 − x2y1 − x3y2 − ... − x1yn |

Using JavaScript the essential line (that gets summed up over all points) is:

let a1 = (pt1.x - pt0.x) * (pt0.y + pt1.y);  // for trapezoid
let a1 = (pt0.x * pt1.y - pt0.y * pt1.x);  // for shoelace

I calculated the area of a regular pentagon 1,000,000 times and both methods took about 43ms. I imagine the browser came up with the same underlying code for both cases!



5288, 5289, 5290, 5291, 5292, 5293, 5294, 5295, 1762, 1763
Geometry Index