Parallel Lines, and Pairs of Angles
Parallel Lines
Lines are parallel if they are always the same distance apart (called "equidistant"), and never meet. Just remember:
Always the same distance apart and never touching.
The red line is parallel to the blue line in each of these examples:
Example 1
Example 2
Parallel lines also point in the same direction.
Parallel lines have so much in common. It's a shame they will never meet!
Try it yourself:
images/geom-parallel.js
Pairs of Angles
When parallel lines are crossed by another line (called a Transversal), special angle relationships appear.
In this example, many angles are equal and form pairs of angles with unique names.
Click on each name below to see it highlighted:
images/parallel-pair.js
Now play with it here. Try dragging the points, and choosing different angle types. You can also turn "Parallel" off or on:
images/geom-line-para.js?mode=corr
Testing for Parallel Lines
Some of these special angle pairs can be used to test if lines really are parallel:
|
|||||||||||||||||||||
Examples
| These lines are parallel, because a pair of Corresponding Angles are equal. | 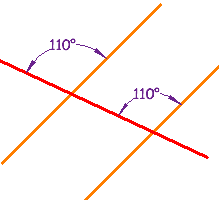 |
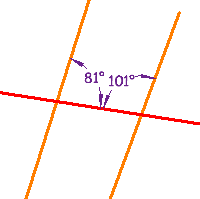 |
These lines are not parallel, because a pair of Consecutive Interior Angles do not add up to 180° (81° + 101° =182°) |
| These lines are parallel, because a pair of Alternate Interior Angles are equal | 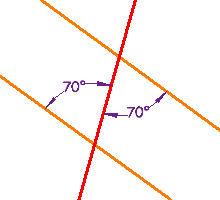 |
813, 814, 1783, 3298, 815, 816, 1784, 1785, 3299, 3300