Pencils and Jars Solution

A solution to the Pencils and Jars Puzzle

pencils

The Puzzles

Puzzle 1

I have some pencils and some jars.
If I put 4 pencils into each jar I will have one jar left over.
If I put 3 pencils into each jar I will have one pencil left over.
How many pencils and how many jars?

Puzzle 2

Again I have some pencils and some jars
If I put 9 pencils into each jar I will have two jars left over
If I put 6 pencils into each jar I will have three pencils left over
How many pencils and how many jars?

A Solution

Puzzle 1 can be solved simply by trying some different numbers.

But if we want to solve Puzzle 2 it is a bit more tricky.

So we will solve Puzzle 1 using Algebra, to make it easier to tackle Puzzle 2.

Puzzle 1

The first stage is to read the question carefully:

I have some pencils and some jars.
If I put 4 pencils into each jar I will have one jar left over
If I put 3 pencils into each jar I will have one pencil left over
How many pencils and how many jars?

There are two distinct statements.

When there are four pencils in each jar there will be one jar left over.

We can say that the number of jars is equal to the number of pencils divided by four plus another one.

This can be expressed using algebra:

j = (p/4) + 1

When there are 3 pencils in each jar there will be one pencil left.

We now need to calculate how many pencils there are.

We can say that the number of pencils will be equal to the number of jars times three plus another one.

Using algebra again we have:

p = 3j + 1

We have ended up with two linear equations.

There are two ways to solve these: Graphically or using simultaneous equations. We will use graphs!

First rearrange the formula to make j the subject:

j = (p/4) + 1 (equation 1)

j = (p − 1) ÷ 3 (equation 2)

Plotting these on a graph using x=p and y=j;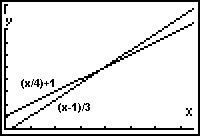
If we find the intersection point we have our answer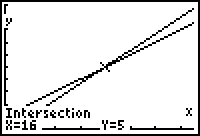

And that is it: there are 16 pencils and 5 Jars.

Puzzle 2

Ahh! That is for YOU to work out, using the same method I have just shown you.