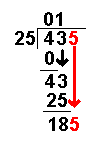
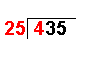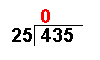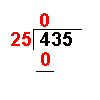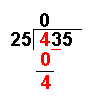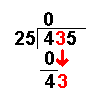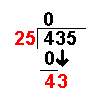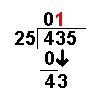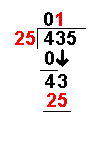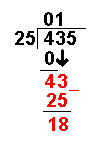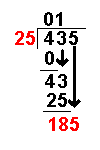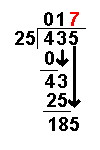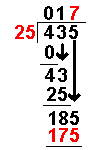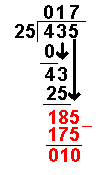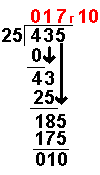Long Division with Remainders

When we are given a long division to do it will not always work out to a whole number.

Sometimes there are numbers left over. These are called remainders.

Taking an example similar to that on the Long Division page it becomes more clear:

(If you feel happy with the process on the Long Division page you can skip the first bit.)

	4 ÷ 25 = 0 remainder 4	The first number of the dividend is divided by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 0 = 0	The answer from the first operation is multiplied by the divisor. The result is placed under the number divided into.
	4 − 0 = 4	Now we take away the bottom number from the top number.
		Bring down the next number of the dividend.
	43 ÷ 25 = 1 remainder 18	Divide this number by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 1 = 25	The answer from the above operation is multiplied by the divisor. The result is placed under the last number divided into.
	43 − 25 = 18	Now we take away the bottom number from the top number.
		Bring down the next number of the dividend.
	185 ÷ 25 = 7 remainder 10	Divide this number by the divisor.
		The whole number result is placed at the top. Any remainders are ignored at this point.
	25 × 7 = 175	The answer from the above operation is multiplied by the divisor. The result is placed under the number divided into.
	185 − 175 = 10	Now we take away the bottom number from the top number.
		There is still 10 left over but no more numbers to bring down.
		With a long division with remainders the answer is expressed as 17 remainder 10 as shown in the diagram   Answer: 435 ÷ 25 = 17 R 10