Interest (An Introduction)
Interest: how much is paid for the use of money (as a percent, or an amount)
Money is Not Free to Borrow
People can always find a use for money, so it costs to borrow money.
How Much does it Cost to Borrow Money?
It depends who you borrow from, when, for how long, and how much.
But they usually charge this way:
 |
As a percent (per year) of the amount borrowed |
 |
|
It is called Interest |
||
Example: Borrow $1,000 from the Bank

Alex wants to borrow $1,000. The local bank says "10% Interest". So to borrow the $1,000 for 1 year will cost:
$1,000 × 10% = $100
In this case the "Interest" is $100, and the "Interest Rate" is 10% (but people often say "10% Interest" without saying "Rate")
Alex will also have to pay back the original $1,000 after one year, so this is what happens:
 |
|
| Alex Borrows $1,000, but has to pay back $1,100 |
This is the idea of Interest ... paying for the use of the money.
 |
Note: This example is a simple full year loan, but banks often want the loan paid back in monthly amounts, and they also charge extra fees! |
Words
There are special words used when borrowing money, as shown here:
Alex is the Borrower, the Bank is the Lender
The Principal of the Loan is $1,000
The Interest is $100
More Than One Year ...
What if Alex wanted to borrow the money for 2 Years?
Simple Interest
If the bank charges "Simple Interest" then Alex just pays another 10% for the extra year.
Alex pays Interest of ($1,000 × 10%) x 2 Years = $200
That is how simple interest works ... pay the same amount of interest every year.
Example: Alex borrows $1,000 for 5 Years, at 10% simple interest:
• Interest = $1,000 × 10% x 5 Years = $500
• Plus the Principal of $1,000 means Alex needs to pay $1,500 after 5 Years
Example: Alex borrows $1,000 for 7 Years, at 6% simple interest:
• Interest = $1,000 × 6% x 7 Years = $420
• Plus the Principal of $1,000 means Alex needs to pay $1,420 after 7 Years
There is a formula for simple interest:
I = Prt
where:
- I = interest
- P = amount borrowed (called "Principal")
- r = interest rate
- t = time
Like this:
Example: Jan borrowed $3,000 for 4 Years at 5% interest rate, how much interest is that?
| I = | Prt |
| I = | $3,000 × 5% × 4 years |
| I = | $3000 × 0.05 × 4 |
| I = | $600 |
But banks almost NEVER charge simple interest, they prefer Compound Interest:
Compound Interest
The bank says "If you paid me everything back after one year, and then I loaned it to you again, I would be loaning you $1,100 for the second year! so I want more interest":
And Alex pays $110 interest in the second year, not just $100.
Because Alex is paying 10% on $1,100 not just $1,000
This may seem unfair ... but imagine YOU lend the money to Alex. After a year you think "Alex owes me $1,100 now, and is still using my money, I should get more interest!"
And so this is the normal way of calculating interest. It is called compounding.
With compounding we work out the interest for the first period, add it the total, and then calculate the interest for the next period, and so on ..., like this:
It is like paying interest on interest: after a year Alex owed $100 interest, the Bank thinks of that as another loan and charges interest on it, too.
After a few years it can get really large. This is what happens on a 5 Year Loan:
|
Year |
Loan at Start |
Interest |
Loan at End |
|---|---|---|---|
|
0 (Now) |
$1,000.00 |
($1,000.00 × 10% = ) $100.00 |
$1,100.00 |
|
1 |
$1,100.00 |
($1,100.00 × 10% = ) $110.00 |
$1,210.00 |
|
2 |
$1,210.00 |
($1,210.00 × 10% = ) $121.00 |
$1,331.00 |
|
3 |
$1,331.00 |
($1,331.00 × 10% = ) $133.10 |
$1,464.10 |
|
4 |
$1,464.10 |
($1,464.10 × 10% = ) $146.41 |
$1,610.51 |
|
5 |
$1,610.51 |
So, after 5 Years Alex has to pay back $1,610.51
And the Interest for the last year was $146.41 ... it sure grew quickly!
(Compare that to the Simple Interest of only $100 each year)
What is Year 0?
Year 0 is the year that starts with the "Birth" of the Loan, and ends just before the 1st Birthday.
Just like when a baby is born its age is zero, and will not be 1 year old until the first birthday.
So the start of Year 1 is the "1st Birthday". And the start of Year 5 is exactly when the loan is 5 years old.
In Summary:
To calculate compound interest, work out the interest for the first period, add it on, and then calculate the interest for the next period, etc.
(There are quicker methods, see Compound Interest)
Why Borrow?
Well ... you may want to buy something you like. Paying it back will end up costing you more though.
But a business may be able to use the money to make even more money.

Example: Chicken Business
You borrow $1,000 to start a chicken business (to buy chicks, chicken food and so on).
A year later you sell all the grown chickens for $1,200.
You pay back the bank $1,100 (the original $1,000 plus 10% interest) and you are left with $100 profit.
And you used someone else's money to do it!
But be careful! What if you only sold the chickens for $800? ... the bank still wants $1,100 and you end up with a $300 loss.
Investment
Compound Interest can work for you!
Investment is when you put money where it can grow, such as a bank, or a business.
If you invest your money at a good interest rate it can grow very nicely.
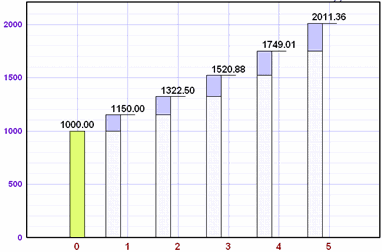
This is what 15% interest on $1,000 can do:
|
Year |
Loan at Start |
Interest |
Loan at End |
|---|---|---|---|
|
0 (Now) |
$1,000.00 |
($1,000.00 × 15% = ) $150.00 |
$1,150.00 |
|
1 |
$1,150.00 |
($1,150.00 × 15% = ) $172.50 |
$1,322.50 |
|
2 |
$1,322.50 |
($1,322.50 × 15% = ) $198.38 |
$1,520.88 |
|
3 |
$1,520.88 |
($1,520.88 × 15% = ) $228.13 |
$1,749.01 |
|
4 |
$1,749.01 |
($1,749.01 × 15% = ) $262.35 |
$2,011.36 |
|
5 |
$2,011.36 |
It more than doubles in 5 Years!
An investment at 15% is not likely to be safe (see Investing introduction) ... but it does show us the power of compounding.
The graph of that investment looks like this:
Maybe you don't have $1,000? Here is what saving $200 every year for 10 Years at 10% interest can do:
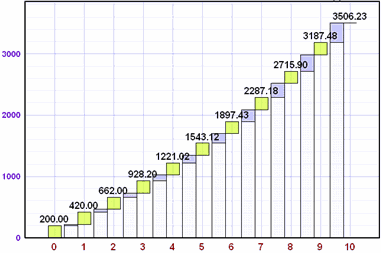
$3,506.23 after 10 Years!
For 10 Years of $200 each year.
Less Than One Year ...
Interest is not always charged yearly. It can be charged Semi-annually (every 6 months), Monthly, even Daily!
But the same rules apply:
- For simple interest: work out the interest for one period, and multiply by the number of periods.
- For compound interest: work out the interest for the first period, add it on and then calculate the interest for the next period, etc.