Internal Rate of Return (IRR)

The Internal Rate of Return is a good way of judging an investment. The bigger the better!

The Internal Rate of Return is the interest rate
that makes the Net Present Value zero

OK, that needs some explaining, right?

It is an Interest Rate.

We find it by first guessing what it might be (say 10%), then work out the Net Present Value.

The Net Present Value is how much the investment is worth in today's money
(we find how to calculate it later)

Then keep guessing (maybe 8%? 9%?) and calculating, until we get a Net Present Value of zero.

Freshly baked muffins in a basket

Example: Sam is going to start a small bakery!

Sam estimates all the costs and earnings for the next 2 years, and calculates the Net Present Value:

At 6% Sam gets a Net Present Value of $2000

But the Net Present Value should be zero, so Sam tries 8% interest:

At 8% Sam gets a Net Present Value of −$1600

Now it's negative! So Sam tries once more, but with 7% interest:

At 7% Sam gets a Net Present Value of $15

Close enough to zero, Sam doesn't want to calculate any more.

The Internal Rate of Return (IRR) is about 7%

So the key to the whole thing is ... calculating the Net Present Value!

Equation: Net Present Value equals the sum of Present Values of all cash flows

Read Net Present Value ... or this quick summary:

Stack of gold coins with a plus sign

An investment has money going out (invested or spent), and money coming in (profits, dividends and so on). We hope more comes in than goes out, and we make a profit!

To get the Net Present Value:

Add what comes in and subtract what goes out,
but future values must be brought back to today's values.

Why?

Because money now is more valuable than money later on.

Example: Let's say you can get 10% interest on your money.

So $1,000 now earns $1,000 x 10% = $100 in a year.

Your $1,000 now becomes $1,100 in a year's time.

(In other words: $1,100 next year is only worth $1,000 now.)

So just work out the Present Value of every amount, then add and subtract them to get the Net Present Value.

Present Value

Timeline showing 1000 dollars today growing to 1100 dollars in one year at 10 percent interest
So $1,000 now is the same as $1,100 next year (at 10% interest).

The Present Value of $1,100 next year is $1,000

Present Value has a detailed explanation, but let's skip straight to the formula:

PV = FV / (1+r)ⁿ

PV is Present Value
FV is Future Value
r is the interest rate (as a decimal, so 0.10, not 10%)
n is the number of years

And let's use the formula:

Handshake representing a financial agreement or promise

Example: Alex promises you $900 in 3 years, what's the Present Value (using a 10% interest rate)?

The Future Value (FV) is $900,
The interest rate (r) is 10%, which is 0.10 as a decimal, and
The number of years (n) is 3

So the Present Value of $900 in 3 years is:

PV = FV / (1+r)ⁿ

PV = $900 / (1 + 0.10)³

PV = $900 / 1.10³

PV = $676.18 (to nearest cent)

Notice that $676.18 is a lot less than $900.

It is saying that $676.18 now is as valuable as $900 in 3 years (at 10%).

Example: try that again, but use an interest rate of 6%

The interest rate (r) is now 6%, which is 0.06 as a decimal:

PV = FV / (1+r)ⁿ

PV = $900 / (1 + 0.06)³

PV = $900 / 1.06³

PV = $755.66 (to nearest cent)

When we only get 6% interest, then $755.66 now is as valuable as $900 in 3 years.

Net Present Value (NPV)

Now we are equipped to calculate the Net Present Value.

For each amount (either coming in, or going out) work out its Present Value, then:

Add the Present Values you receive
Subtract the Present Values you pay

We'll use this sign rule: money we pay is negative (−) and money we receive is positive (+).

Like this:

Example: You invest $500 now, and get back $570 next year. Use an Interest Rate of 10% to work out the NPV.

Money Out: $500 now

You invest $500 now, so PV = −$500.00

Money In: $570 next year

PV = $570 / (1+0.10)¹ = $570 / 1.10

PV = $518.18 (to nearest cent)

And the Net Amount is:

Net Present Value = $518.18 − $500.00 = $18.18

So, at 10% interest, that investment has NPV = $18.18

But your choice of interest rate can change things!

Example: Same investment, but work out the NPV using an Interest Rate of 15%

Money Out: $500 now

You invest $500 now, so PV = −$500.00

Money In: $570 next year:

PV = $570 / (1+0.15)¹ = $570 / 1.15

PV = $495.65 (to nearest cent)

Work out the Net Amount:

Net Present Value = $495.65 - $500.00 = −$4.35

So, at 15% interest, that investment has NPV = −$4.35

It has gone negative!

Now it gets interesting ... what Interest Rate can make the NPV exactly zero? Let's try 14%:

Example: Try again, but the interest Rate is 14%

Money Out: $500 now

You invest $500 now, so PV = −$500.00

Money In: $570 next year:

PV = $570 / (1+0.14)¹ = $570 / 1.14

PV = $500 (exactly)

Work out the Net Amount:

Net Present Value = $500 − $500.00 = $0

Exactly zero!

At 14% interest NPV = $0

And we have discovered the Internal Rate of Return ... it is 14% for that investment.

Because 14% made the NPV zero.

Internal Rate of Return

So the Internal Rate of Return is the interest rate that makes the Net Present Value zero.

And that "guess and check" method is the common way to find it (though in that simple case it could have been worked out directly).

Let's try a bigger example:

Example: Invest $2,000 now, receive 3 yearly payments of $100 each, plus $2,500 in the 3rd year.

Let's try 10% interest:

Now: PV = −$2,000
Year 1: PV = $100 / 1.10 = $90.91
Year 2: PV = $100 / 1.10² = $82.64
Year 3: PV = $100 / 1.10³ = $75.13
Year 3 (final payment): PV = $2,500 / 1.10³ = $1,878.29

Adding those up gets:

NPV = −$2,000 + $90.91 + $82.64 + $75.13 + $1,878.29 = $126.97

Let's try a better guess, say 12% interest rate:

Example: (continued) at 12% interest rate

Now: PV = −$2,000
Year 1: PV = $100 / 1.12 = $89.29
Year 2: PV = $100 / 1.12² = $79.72
Year 3: PV = $100 / 1.12³ = $71.18
Year 3 (final payment): PV = $2,500 / 1.12³ = $1,779.45

Adding those up gets:

NPV = −$2,000 + $89.29 + $79.72 + $71.18 + $1,779.45 = $19.64

Ooh .. so close. Maybe 12.4% ?

Example: (continued) at 12.4% interest rate

Now: PV = −$2,000
Year 1: PV = $100 / 1.124 = $88.97
Year 2: PV = $100 / 1.124² = $79.15
Year 3: PV = $100 / 1.124³ = $70.42
Year 3 (final payment): PV = $2,500 / 1.124³ = $1,760.52

Adding those up gets:

NPV = −$2,000 + $88.97 + $79.15 + $70.42 + $1,760.52 = −$0.94

That's good enough! Let's stop there and say the Internal Rate of Return is 12.4%

In a way it is saying "this investment could earn 12.4%" (assuming it all goes according to plan!).

Note: Some investments can have more than one IRR, or no IRR.

This can happen when the cashflows change sign more than once (for example: pay out, then receive, then pay again).

In those cases, it is safer to compare investments using NPV.

Using the Internal Rate of Return (IRR)

The IRR is a good way of judging different investments.

First of all, the IRR should be higher than the cost of funds. If it costs you 8% to borrow money, then an IRR of only 6% isn't good enough!

It is also useful when investments are quite different.

Maybe the amounts involved are quite different
Or maybe one has high costs at the start, and another has many small costs over time
and so on...

Example: instead of investing $2,000 like above, you could also invest 3 yearly sums of $1,000 to gain $4,000 in the 4th year ... should you do that instead?

I did this one in a spreadsheet, and found that 10% was pretty close:

Spreadsheet table showing cash flows and an NPV calculation approaching zero

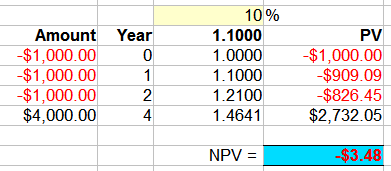
At 10% interest rate NPV = −$3.48

So the Internal Rate of Return is about 10%

And so the other investment (where the IRR was 12.4%) is better.

Doing your calculations in a spreadsheet is great as you can easily change the interest rate until the NPV is zero.

You also get to see the influence of all the values, and how sensitive the results are to changes (which is called "sensitivity analysis").