Pythagorean Triples
A "Pythagorean Triple" is a set of positive integers, a, b and c that fits the rule:
a2 + b2 = c2
Example: The smallest Pythagorean Triple is 3, 4 and 5.
Let's check it:
32 + 42 = 52
Calculating this becomes:
9 + 16 = 25
Yes, it is a Pythagorean Triple!
Triangles
When a triangle's sides are a Pythagorean Triple it is a right angled triangle.
See Pythagoras' Theorem for more details.
Example: The Pythagorean Triple of 3, 4 and 5 makes a Right Angled Triangle:

Here are two more Pythagorean Triples:
| 5, 12, 13 | 9, 40, 41 | |
 |
 |
|
| 52 + 122 = 132 | 92 + 402 = 412 | |
| 25 + 144 = 169 | (try it yourself) |
And each triangle has a right angle!
List of the First Few
Here is a list of the first few Pythagorean Triples (not including "scaled up" versions mentioned below):
| (3, 4, 5) | (5, 12, 13) | (7, 24, 25) | (8, 15, 17) |
| (9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (15,112,113) | (16, 63, 65) | (17,144,145) | (19,180,181) |
| (20, 21, 29) | (20, 99,101) | (21,220,221) | (23,264,265) |
| (24,143,145) | (25,312,313) | (27,364,365) | (28, 45, 53) |
| (28,195,197) | (29,420,421) | (31,480,481) | (32,255,257) |
| (33, 56, 65) | (33,544,545) | (35,612,613) | (36, 77, 85) |
| (36,323,325) | (37,684,685) | ... infinitely many more ... | |
Scale Them Up
The simplest way to create further Pythagorean Triples is to scale up a set of triples.
Example: scale 3, 4, 5 by 2 gives 6, 8, 10
Which also fits the formula a2 + b2 = c2:
62 + 82 = 102
36 + 64 = 100
If you want to know more about them read Pythagorean Triples - Advanced
Useful
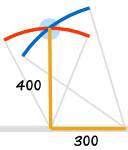
We can use these triples to make a right angle in the real world (such as with carpentry, tiling, etc)
The simple (3,4,5 triple) is the easiest to remember.
And if you need a triple with two nearly equal sides use (119,120,169) or (696,697,985).


