Ydhb3q2lG6E

Asymptote

An asymptote is a line that a curve approaches, as it heads toward infinity:

Curve approaching a dashed horizontal line as it goes to the right

Types

There are three types: horizontal, vertical and oblique:

Three graphs showing horizontal, vertical, and oblique dashed lines being approached by curves

The direction can also be negative:

Graph showing a curve approaching a dashed line as x goes to negative infinity

The curve can approach from either side (such as from above or below for a horizontal asymptote),

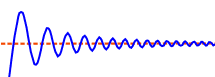
Curve oscillating across a horizontal dashed line before settling near it

or may actually cross over (possibly many times), and even move away and back again.

The important point is that:

The distance between the curve and the asymptote tends to zero as they head to infinity (or −infinity)

It is a horizontal asymptote when:

as x goes to infinity (or −infinity) the curve approaches some constant value b

It is a vertical asymptote when:

as x approaches some constant value c (from the left or right) then the curve goes toward infinity (or −infinity).

It is an oblique asymptote when:

as x goes to infinity (or −infinity) then the curve goes toward a line y=mx+b

(note: m isn't zero as that's a horizontal asymptote).

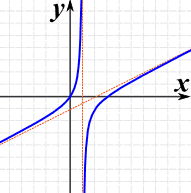
xy graph of (x^2-3x)/(2x-2)

The graph of (x²−3x)/(2x−2) has:

Play with it here:

images/function-graph.js?fn0=(x^2-3x)/(2x-2);fn1=x/2-1;xmin=-12;xmax=12;ymin=-8;ymax=8

These questions will only make sense when you know Rational Expressions:

8432, 8434, 9666, 9667, 9668, 8433, 8435, 8436, 8437, 9669