Solving SAS Triangles

Example 1

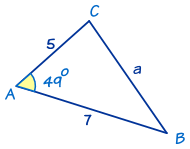
In this triangle we know:

• angle A = 49°
• b = 5
• and c = 7

 

To solve the triangle we need to find side a and angles B and C.

This type is not quite so easy. We only know one angle, so we have to find the third side of the triangle first. However, we also don't know the angles facing the other two sides, so we can't use The Law of Sines.

We must use The Law of Cosines to find side a first:

a² = b² + c² - 2bccosA

So a = √28.075...

Now we can find either angle B or angle C by using The Law of Sines. Let's find C first:

Did you notice that we didn't use a = 5.30. That number is rounded to 2 decimal places. It's much better to use the unrounded number 5.298... which you should still have on your calculator screen from the last calculation.

So sin C = (sin(49°)×7)/5.298...

And C = sin^-1(0.9970...)

Now all we have left to find is angle B. We could use The Law of Sines again to find B. However, it's much easier to use 'angles of a triangle add to 180°':

Now we have completely solved the triangle i.e. we have found all its angles and sides.

Example 2

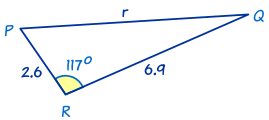
This is also an SAS triangle.

First of all we will find r using The Law of Cosines:

r² = p² + q² - 2pq cos R

So a = √70.659...

Now we will find angle P by using The Law of Sines:

sin P / p = sin R / r

So sin P/6.9 = sin(117°)/8.405...

So sin P = (sin(117°)×6.9)/8.405...

So P = 47.0° correct to one decimal place.

Now we will find angle Q using 'angles of a triangle add to 180°':

So Q = 180° - 117° - 47.0°