Solving SSS Triangles

"SSS" means "Side, Side, Side"

When you know three sides of the triangle, and want to find the missing angles.

To solve an SSS triangle:

use The Law of Cosines first to calculate one of the angles
then use The Law of Cosines again to find another angle
and finally use angles of a triangle add to 180° to find the last angle.

Example 1

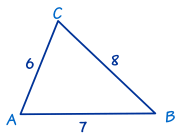
In this triangle we know the three sides:

a = 8,
b = 6 and
c = 7.

Use The Law of Cosines first to find one of the angles. It doesn't matter which one. Let's find angle A first:

cos A = (b² + c² - a²)/2bc

= (6² + 7² - 8²)/(2×6×7) = (36 + 49 - 64)/84 = 21/84 = 0.25

A = cos^-1(0.25)

= 75.5° correct to one decimal place.

Next we will find another side. We use The Law of Cosines again, this time for angle B:

cos B = (c² + a² - b²)/2ca

= (7² + 8² - 6²)/(2×7×8) = (49 + 64 - 36)/112 = 77/112 = 0.6875

So B = 46.5674...°

= 46.6° correct to one decimal place.

Finally, we can find angle C by using 'angles of a triangle add to 180°':

So C = 180° - 75.5224...° - 46.5674...°

= 57.9° correct to one decimal place.

Now we have completely solved the triangle i.e. we have found all its angles.

Example 2

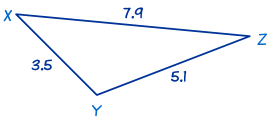
This is also an SSS triangle.

In this triangle we know the three sides x = 5.1, y = 7.9 and z = 3.5. Use The Law of Cosines to find angle X first:

cos X = (y² + z² - x²)/2yz

= ((7.9)² + (3.5)² - (5.1)²)/(2×7.9×3.5)

= (62.41 + 12.25 - 26.01)/55.3

= 48.65/55.3 = 0.8797...

So X = cos^-1(0.8797...)

= 28.3881...°

= 28.4° correct to one decimal place.

Next we will use The Law of Cosines again to find angle Y:

cosY = (z² + x² - y²)/2zx

= ((3.5)² + (5.1)² - (7.9)²)/(2×3.5×5.1)

= (12.25 + 26.01 - 62.41)/35.7

= -24.15/35.7 = -0.6764...

So Y = cos^-1(-0.6764...)

= 132.5684...°

= 132.6° correct to one decimal place.

Finally, we can find angle Z by using 'angles of a triangle add to 180°':

So Z = 180° - 28.3881...° - 132.5684...°

= 19.0° correct to one decimal place.

Another Method

Here is another (slightly faster) way to solve an SSS triangle:

use The Law of Cosines first to calculate the largest angle
then use The Law of Sines to find another angle
and finally use angles of a triangle add to 180° to find the last angle.

Largest Angle?

Why do we try to find the largest angle first? That way the other two angles must be acute (less than 90°) and the Law of Sines will give correct answers.

You see, the Law of Sines is difficult to use with angles above 90°. There can be two answers either side of 90° (example: 95° and 85°), but your calculator will only give you the smaller one.

So by calculating the largest angle first using the Law of Cosines, the remaining angles will be less than 90° and the Law of Sines can be used on either of them without difficulty.

Example 3

B is the largest angle, so find B first using the Law of Cosines:

cos B = (a² + c² – b²) / 2ac

cos B = (11.6² + 7.4² – 15.2²) / (2×11.6×7.4)

cos B = (134.56 + 54.76 – 231.04) / 171.68

cos B = -41.72 / 171.68

cos B = -0.2430...

B = 104.1°

Use the Law of Sines, sinC/c = sinB/b, to find angle A:

sin C / 7.4 = sin 104.1° / 15.2

sin C = (7.4 sin 104.1°) / 15.2 = 0.4722...

C = 28.2°

Find angle A using "angles of a triangle add to 180":

A = 180° - (104.1° + 28.2°)

A = 180° - 132.3°

A = 47.7°

Therefore A = 47.7°, B = 104.1°, and C = 28.2°