Dot Product
A vector has magnitude (how long it is) and direction:
Here are two vectors:
They can be multiplied using the "Dot Product" (also see Cross Product).
Calculating
The Dot Product is written using a central dot:
a · b
This means the Dot Product of a and b
We can calculate the Dot Product of two vectors this way:
a · b = |a| × |b| × cos(θ)
Where:
|a| is the magnitude (length) of vector a
|b| is the magnitude (length) of vector b
θ is the angle between a and b
So we multiply the length of a times the length of b, then multiply by the cosine of the angle between a and b
OR we can calculate it this way:
a · b = ax × bx + ay × by
So we multiply the x's, multiply the y's, then add.
Both methods work!
And the result is a number (called a "scalar" to show it is not a vector).
Example: Calculate the dot product of vectors a and b:
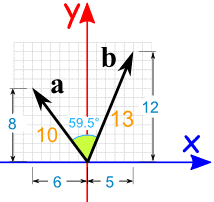
a · b = |a| × |b| × cos(θ)
OR we can calculate it this way:
a · b = ax × bx + ay × by
Both methods came up with the same result (after rounding)
Also note that we used minus 6 for ax (it is heading in the negative x-direction)
Note: you can use the Vector Calculator to help you.
Why cos(θ) ?
OK, to multiply two vectors it makes sense to multiply their lengths together but only when they point in the same direction.
So we make one "point in the same direction" as the other by multiplying by cos(θ):
We take the component of a
that lies alongside b
Like shining a light to see
where the shadow lies
THEN we multiply !
It works exactly the same if we "projected" b alongside a then multiplied.
Because it doesn't matter which order we do the multiplication:
|a| × |b| × cos(θ) = |a| × cos(θ) × |b|
In effect, the dot product multiplies the aligned lengths.
Remembering Cos
To remember to multiply by cos(θ) think "dot cos".
Right Angles
When two vectors are at right angles to each other the dot product is zero.
Example: calculate the dot product for:
a · b = |a| × |b| × cos(θ)
or we can calculate it this way:
a · b = ax × bx + ay × by
This can be a handy way to find out if two vectors are at right angles.
Same Direction
The dot product of two vectors that point in the same direction is the simple product of their lengths, because the angle is 0 degrees which has a cosine of 1
Right-Angled Triangle
Let's use the dot product on a right-angled triangle!
We just proved the Pythagorean Theorem!
Note: when we allow angles other than 90 degrees we can create the Law of Cosines. Have a go yourself, but be careful how you define the angle!
Physics
The Dot Product is used a lot in Physics
Example: Work
In Physics Work is force times distance, but only the aligned part.
So work is the dot product of force and distance.
Alex pushes a box 3 m straight forward using 200 N of force. But his push is a little upwards by 20°.
(Without cos θ, the wrong value would be 600 J)
Three or More Dimensions
This all works fine in 3 (or more) dimensions, too.
And can actually be very useful!
Example: Sam has measured the end-points of two poles, and wants to know the angle between them:
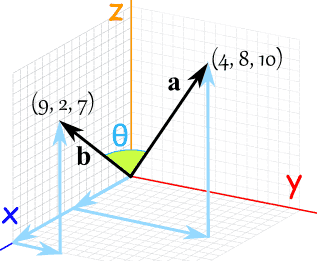
We have 3 dimensions, so don't forget the z-components:
a · b = ax × bx + ay × by + az × bz
Now for the other formula:
a · b = |a| × |b| × cos(θ)
But what is |a| ? It is the magnitude, or length, of the vector a. We can use Pythagoras:
- |a| = √(42 + 82 + 102)
- |a| = √(16 + 64 + 100)
- |a| = √180
Likewise for |b|:
- |b| = √(92 + 22 + 72)
- |b| = √(81 + 4 + 49)
- |b| = √134
And we know from the calculation above that a · b = 122, so:
a · b = |a| × |b| × cos(θ)
Done!
I tried a calculation like that once, but worked all in angles and distances ... it was very hard, involved lots of trigonometry, and my brain hurt. The method above is much easier.
Cross Product
The Dot Product gives a scalar (ordinary number) answer, and is sometimes called the scalar product.
But there is also the Cross Product which gives a vector as an answer, and is sometimes called the vector product.
