Solving Word Questions
With LOTS of examples!
In Algebra we often have word questions like:
Example: Sam and Alex play tennis.
On the weekend Sam played 4 more games than Alex did, and together they played 12 games.
How many games did Alex play?
How do we solve them?
The trick is to break the solution into two parts:
Turn the English into Algebra.
Then use Algebra to solve.
Turning English into Algebra
To turn the English into Algebra it helps to:
- Read the whole thing first
- Do a sketch if possible
- Assign letters for the values
- Find or work out formulas
You should also write down what is actually being asked for, so you know where you are going and when you have arrived!
Also look for key words:
| When you see | Think | |
|---|---|---|
|
add, total, sum, increase, more, combined, together, plus, more than |
+ | |
|
minus, less, difference, fewer, decreased, reduced |
− | |
|
multiplied, times, of, product, factor |
× | |
|
divided, quotient, per, out of, ratio, percent, rate |
÷ | |
| maximize or minimize | geometry formulas |
|
| rate, speed | distance formulas |
|
| how long, days, hours, minutes, seconds | time |
Thinking Clearly
Some wording can be tricky, making it hard to think "the right way around", such as:
Example: Sam has 2 dollars less than Alex. How do we write this as an equation?
- Let S = dollars Sam has
- Let A = dollars Alex has
Now ... is that: S − 2 = A
or should it be: S = A − 2
or should it be: S = 2 − A
The correct answer is S = A − 2
(S − 2 = A is a common mistake, as the question is written "Sam ... 2 less ... Alex")
Example: on our street there are twice as many dogs as cats. How do we write this as an equation?
- Let D = number of dogs
- Let C = number of cats
Now ... is that: 2D = C
or should it be: D = 2C
Think carefully now!
The correct answer is D = 2C
(2D = C is a common mistake, as the question is written "twice ... dogs ... cats")
Examples
Let's start with a really simple example so we see how it's done:
Example: A rectangular garden is 12m by 5m, what is its area?
Turn the English into Algebra:
Sketch:
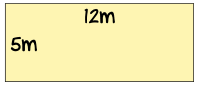
Letters:
- Use w for width of rectangle: w = 12m
- Use h for height of rectangle: h = 5m
Formula for Area of a Rectangle: A = w × h
We are being asked for the Area.
Solve:
A = w × h = 12 × 5 = 60 m2
The area is 60 square meters.
Now let's try the example from the top of the page:

Example: Sam and Alex play Tennis. On the weekend Sam played 4 more games than Alex did, and together they played 12 games. How many games did Alex play?
Turn the English into Algebra:
Letters:
- Use S for how many games Sam played
- Use A for how many games Alex played
We know that Sam played 4 more games than Alex, so: S = A + 4
And we know that together they played 12 games: S + A = 12
We are being asked for how many games Alex played: A
Solve:
substitute "A + 4" for S:(A + 4) + A = 12
Which means that Alex played 4 games of tennis.
Check: Sam played 4 more games than Alex, so Sam played 8 games. Together they played 8 + 4 = 12 games. Yes!
A slightly harder example:

Example: Alex and Sam also build tables.
Together they make 10 tables in 12 days.
Alex working alone can make 10 in 30 days.
How long would it take Sam working alone to make 10 tables?
Turn the English into Algebra:
Letters:
- Use a for Alex's work rate
- Use s for Sam's work rate
12 days of Alex and Sam is 10 tables, so: 12a + 12s = 10
30 days of Alex alone is also 10 tables: 30a = 10
We are being asked how long it would take Sam to make 10 tables.
Solve:
30a = 10, so Alex's rate (tables per day) is: a = 10/30 = 1/3
Which means that Sam's rate is half a table a day (faster than Alex!)
So 10 tables would take Sam just 20 days.
Should Sam be paid more I wonder?
And another "substitution" example:

Example: Jenna is training hard to qualify for the National Games.
She has a regular weekly routine, training for five hours a day on some days and 3 hours a day on the other days.
She trains altogether 27 hours in a seven day week. On how many days does she train for five hours?
Letters:
- The number of "5 hour" days: d
- The number of "3 hour" days: e
We know there are seven days in the week, so: d + e = 7
And she trains 27 hours in a week, with d 5 hour days and e 3 hour days: 5d + 3e = 27
We are being asked for how many days she trains for 5 hours: d
Solve:
The number of "5 hour" days is 3
Check: She trains for 5 hours on 3 days a week, so she must train for 3 hours a day on the other 4 days of the week.
3 × 5 hours = 15 hours, plus 4 × 3 hours = 12 hours gives a total of 27 hours
Some examples from Geometry:
Example: A circle has an area of 12 mm2, what is its radius?
Letters:
- Use A for Area: A = 12 mm2
- Use r for radius
And the formula for Area is: A = π r2
We are being asked for the radius.
Solve:
We need to rearrange the formula to find the area
Example: A cube has a volume of 125 mm3, what is its surface area?
Make a quick sketch:
Letters:
- Use V for Volume
- Use A for Area
- Use s for side length of cube
Formulas:
- Volume of a cube: V = s3
- Surface area of a cube: A = 6s2
We are being asked for the surface area.
Solve:
First work out s using the volume formula:
Now we can calculate surface area:
An example about Money:

Example: Joel works at the local pizza parlor. When he works overtime he earns 1¼ times the normal rate.
One week Joel worked for 40 hours at the normal rate of pay and also worked 12 hours overtime. If Joel earned $660 altogether in that week, what is his normal rate of pay?
Letters:
- Joel's normal rate of pay: $N per hour
Formulas:
- Joel works for 40 hours at $N per hour = $40N
- When Joel does overtime he earns 1¼ times the normal rate = $1.25N per hour
- Joel works for 12 hours at $1.25N per hour = $(12 × 1¼N) = $15N
- And together he earned $660, so:
$40N + $(12 × 1¼N) = $660
We are being asked for Joel's normal rate of pay $N.
Solve:
So Joel’s normal rate of pay is $12 per hour
Check
Joel’s normal rate of pay is $12 per hour, so his overtime rate is 1¼ × $12 per hour = $15 per hour. So his normal pay of 40 × $12 = $480, plus his overtime pay of 12 × $15 = $180 gives us a total of $660
More about Money, with these two examples involving Compound Interest
Example: Alex puts $2000 in the bank at an annual compound interest of 11%. How much will it be worth in 3 years?
This is the compound interest formula:
So we will use these letters:
- Present Value PV = $2,000
- Interest Rate (as a decimal): r = 0.11
- Number of Periods: n = 3
- Future Value (the value we want): FV
We are being asked for the Future Value: FV
Solve:
Example: Roger deposited $1,000 into a savings account. The money earned interest compounded annually at the same rate. After nine years Roger's deposit has grown to $1,551.33
What was the annual rate of interest for the savings account?
The compound interest formula:
With:
- Present Value PV = $1,000
- Interest Rate (the value we want): r
- Number of Periods: n = 9
- Future Value: FV = $1,551.33
We are being asked for the Interest Rate: r
Solve:
So the annual rate of interest is 5%
Check: $1,000 × (1.05)9 = $1,000 × 1.55133 = $1,551.33
And an example of a Ratio question:
Example: At the start of the year the ratio of boys to girls in a class is 2 : 1
But now, half a year later, four boys have left the class and there are two new girls. The ratio of boys to girls is now 4 : 3
How many students are there altogether now?
Letters:
- Number of boys now: b
- Number of girls now: g
The current ratio is 4 : 3
bg = 43
Which can be rearranged to 3b = 4g
At the start of the year there was (b + 4) boys and (g − 2) girls, and the ratio was 2 : 1
b + 4g − 2 = 21
Which can be rearranged to b + 4 = 2(g − 2)
We are being asked for how many students there are altogether now: b + g
Solve:
There are 12 girls!
And 3b = 4g, so b = 4g/3 = 4 × 12 / 3 = 16, so there are 16 boys
So there are now 12 girls and 16 boys in the class, making 28 students altogether.
Check
There are now 16 boys and 12 girls, so the ratio of boys to girls is 16 : 12 = 4 : 3
At the start of the year there were 20 boys and 10 girls, so the ratio was 20 : 10 = 2 : 1
And now for some Quadratic Equations:
Example: The product of two consecutive even integers is 168. What are the integers?
Consecutive means one after the other. And they are even, so they could be 2 and 4, or 4 and 6, etc.
We will call the smaller integer n, and so the larger integer must be n+2
And we are told the product (what we get after multiplying) is 168, so we know:
n(n + 2) = 168
We are being asked for the integers
Solve:
That is a Quadratic Equation, and there are many ways to solve it. Using the Quadratic Equation Solver we get −14 and 12.
Check −14: −14(−14 + 2) = (−14)×(−12) = 168 YES
Check 12: 12(12 + 2) = 12×14 = 168 YES
So there are two solutions: −14 and −12 is one, 12 and 14 is the other.
Note: we could have also tried "guess and check":
- We could try, say, n=10: 10(12) = 120 NO (too small)
- Next we could try n=12: 12(14) = 168 YES
But unless we remember that multiplying two negatives make a positive we might overlook the other solution of (−14)×(−12).
And:
Example: You are an Architect. Your client wants a room twice as long as it is wide. They also want a 3m wide veranda along the long side.
Your client has 56 square meters of beautiful marble tiles to cover the whole area.
What should the length of the room be?
Let's first make a sketch so we get things right!:
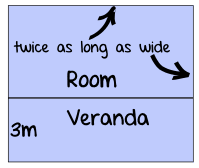
Letters:
- the length of the room: L
- the width of the room: W
- the total Area including veranda: A
We know:
- the width of the room is half its length: W = ½L
- the total area is the (room width + 3) times the length: A = (W+3) × L = 56
We are being asked for the length of the room: L
Solve:
This is a quadratic equation, there are many ways to solve it, this time let's use factoring:
and add to give b=6 are 14 and −8:L2 + 14L − 8L − 112 = 0
And so L = 8 or −14
There are two solutions to the quadratic equation, but only one of them is possible since the length of the room cannot be negative!
So the length of the room is 8 m
Check
L = 8, so W = ½L = 4
So the area of the rectangle = (W+3) × L = 7 × 8 = 56
There we are ...
... I hope these examples will help you get the idea of how to handle word questions. Now how about some practice?


