Implicit Differentiation

Finding the derivative when you can’t solve for y

What are you trying to imply?

You may like to read Introduction to Derivatives and Derivative Rules first.

Implicit vs Explicit

A function can be explicit or implicit:

Explicit: "y = some function of x". When we know x we can calculate y directly.

Implicit: "some function of y and x equals something else". Knowing x does not lead directly to y.

Example: A Circle

Explicit Form		Implicit Form
y = ± √ (r² − x²)		x² + y² = r²
In this form, y is expressed as a function of x.		In this form, the function is expressed in terms of both y and x.

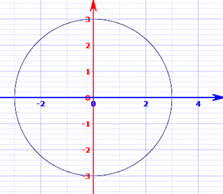
graph x^2 + y^2 = 9, a circle
The graph of x² + y² = 3²

How to do Implicit Differentiation

Differentiate with respect to x
Collect all the dy dx on one side
Solve for dy dx

Example: x² + y² = r²

Differentiate with respect to x:

d dx (x²) + d dx (y²) = d dx (r²)

Let's solve each term:

Use the Power Rule: d dx (x²) = 2x

Use the Chain Rule (explained below): d dx (y²) = 2y dy dx

r² is a constant, so its derivative is 0: d dx (r²) = 0

Which gives us:

2x + 2y dy dx = 0

Collect all the dy dx on one side

y dy dx = −x

Solve for dy dx :

dy dx = −x y

The Chain Rule Using dy dx

Let's look more closely at how d dx (y²) becomes 2y dy dx

The Chain Rule says:

du dx = du dy dy dx

Substitute in u = y²:

d dx (y²) = d dy (y²) dy dx

And then:

d dx (y²) = 2y dy dx

Basically, all we did was differentiate with respect to y and multiply by dy dx

Another common notation is to use ’ to mean d dx

The Chain Rule Using ’

The Chain Rule can also be written using ’ notation:

f(g(x))’ = f’(g(x))g’(x)

g(x) is our function "y", so:

f(y)’ = f’(y)y’

f(y) = y², so f’(y) = 2y:

f(y)’ = 2yy’

or alternatively: f(y)’ = 2y dy dx

Again, all we did was differentiate with respect to y and multiply by dy dx

Explicit

Let's also find the derivative using the explicit form of the equation.

To solve this explicitly, we can solve the equation for y
Then differentiate
Then substitute the equation for y again

Example: x² + y² = r²

Subtract x² from both sides:y² = r² − x²

Square root:y = ±√(r² − x²)

Let's do just the positive: y = √(r² − x²)

As a power: y = (r² − x²)^½

Derivative (Chain Rule):y’ =½(r² − x²)^−½(−2x)

Simplify:y’ = −x(r² − x²)^−½

Simplify more:y’ = −x (r² − x²)^½

Now, because y = (r² − x²)^½: y’ = −x/y

We get the same result this way!

You can try taking the derivative of the negative term yourself.

Chain Rule Again!

Yes, we used the Chain Rule again. Like this (note different letters, but same rule):

dy dx = dy df df dx

Substitute in f = (r² − x²):

d dx (f^½) = d df (f^½) d dx (r² − x²)

Derivatives:

d dx (f^½) = ½(f^−½) (−2x)

And substitute back f = (r² − x²):

d dx (r² − x²)^½ = ½((r² − x²)^−½) (−2x)

And we simplified from there.

Using The Derivative

OK, so why find the derivative y’ = −x/y ?

Well, for example, we can find the slope of a tangent line.

Example: what is the slope of a circle centered at the origin with a radius of 5 at the point (3, 4)?

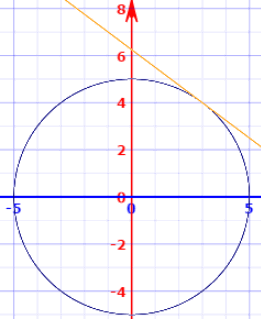
graph x^2 + y^2 = 25 with tangent line

No problem, just substitute it into our equation:

dy dx = −x/y

dy dx = −3/4

And for bonus, the equation for the tangent line is:

y = −3/4 x + 25/4

Another Example

Sometimes the implicit way works where the explicit way is hard or impossible.

Example: 10x⁴ − 18xy² + 10y³ = 48

How do we solve for y? We don't have to!

First, differentiate with respect to x (use the Product Rule for the xy² term).
Then move all dy/dx terms to the left side.
Solve for dy/dx

Like this:

Start with:10x⁴ − 18xy² + 10y³ = 48

Derivative:10 (4x³) − 18(x(2y dy dx ) + y²) + 10(3y² dy dx ) = 0

(the middle term is explained
in "Product Rule" below)

Simplify:40x³ − 36xy dy dx − 18y² + 30y² dy dx = 0

dy dx on left:−36xy dy dx + 30y²dy dx = −40x³ + 18y²

Simplify :(30y²−36xy) dy dx = 18y² − 40x³

Simplify :3(5y²−6xy) dy dx = 9y² − 20x³

And we get:

dydx = 9y² − 20x³3(5y² − 6xy)

Product Rule

For the middle term we used the Product Rule: (fg)’ = f g’ + f’ g

(xy²)’ = x(y²)’ + (x)’y²

= x(2y dy dx ) + y²

Because (y²)’ = 2y dy dx (we worked that out in a previous example)

Oh, and dxdx = 1, in other words x’ = 1

Inverse Functions

Implicit differentiation can help us solve inverse functions.

The general pattern is:

Start with the inverse equation in explicit form. Example: y = sin⁻¹(x)
Rewrite it in non-inverse mode: Example: x = sin(y)
Differentiate this function with respect to x on both sides.
Solve for dy/dx

As a final step we can try to simplify more by substituting the original equation.

An example will help:

Example: the inverse sine function y = sin⁻¹(x)

Start with:y = sin⁻¹(x)

In non−inverse mode:x = sin(y)

Derivative: d dx (x) = d dx sin(y)

1 = cos(y) dy dx

Put dy dx on left: dy dx = 1 cos(y)

We can also go one step further using the Pythagorean identity:

sin² y + cos² y = 1

cos y = √(1 − sin² y )

And, because sin(y) = x (from above!), we get:

cos y = √(1 − x²)

Which leads to:

dy dx = 1 √(1 − x²)

Example: the derivative of square root √x

Start with:y = √x

So:y² = x

Derivative:2y dy dx = 1

Simplify: dy dx = 1 2y

Because y = √x: dy dx = 1 2√x

Note: this is the same answer we get using the Power Rule:

Start with:y = √x

As a power:y = x^½

Power Rule d dx xⁿ = nxⁿ⁻¹: dy dx = (½)x^−½

Simplify: dy dx = 1 2√x

Summary

To Implicitly derive a function (useful when a function can't easily be solved for y)
- Differentiate with respect to x
- Collect all the dy/dx on one side
- Solve for dy/dx
To derive an inverse function, restate it without the inverse then use Implicit differentiation

11312, 11313, 11314, 11315, 11316, 11317, 11318, 11319, 11320, 11321

Implicit Differentiation

Implicit vs Explicit

Example: A Circle

How to do Implicit Differentiation

Example: x2 + y2 = r2

The Chain Rule Using dy dx

Basically, all we did was differentiate with respect to y and multiply by dy dx

The Chain Rule Using ’

Again, all we did was differentiate with respect to y and multiply by dy dx

Explicit

Example: x2 + y2 = r2

Chain Rule Again!

Using The Derivative

Example: what is the slope of a circle centered at the origin with a radius of 5 at the point (3, 4)?

Another Example

Example: 10x4 − 18xy2 + 10y3 = 48

Product Rule

Inverse Functions

Example: the inverse sine function y = sin−1(x)

Example: the derivative of square root √x

Summary

Example: x² + y² = r²

Example: x² + y² = r²

Example: 10x⁴ − 18xy² + 10y³ = 48

Example: the inverse sine function y = sin⁻¹(x)