The Mean from a Frequency Table
It is easy to calculate the Mean:
Add up all the numbers,
then divide by how many numbers there are.
Example: What is the Mean of these numbers?
6, 11, 7
- Add the numbers: 6 + 11 + 7 = 24
- Divide by how many numbers (there are 3 numbers): 24 ÷ 3 = 8
The Mean is 8
But sometimes we don't have a simple list of numbers, it might be a frequency table like this (the "frequency" says how often they occur):
| Score | Frequency |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 4 |
| 4 | 2 |
| 5 | 1 |
(it says score 1 occurred 2 times, score 2 occurred 5 times, and so on)
We could list all the numbers like this:
Mean = 1+1 + 2+2+2+2+2 + 3+3+3+3 + 4+4 + 5(how many numbers)
But instead of lots of adds (like 3+3+3+3) it is easier to use multiplication:
Mean = 2×1 + 5×2 + 4×3 + 2×4 + 1×5 (how many numbers)
And instead of counting how many numbers, we can add up the frequencies:
Mean = 2×1 + 5×2 + 4×3 + 2×4 + 1×5 2 + 5 + 4 + 2 + 1
So now we calculate:
Mean = 2 + 10 + 12 + 8 + 5 14
= 3714 = 2.64...
And that is how to calculate the mean from a frequency table!
Here is another example:
Example: Parking Spaces per House in Hampton Street
Isabella went up and down the street to discover how many parking spaces each house has. Here are her results:
| Parking Spaces |
Frequency |
|---|---|
| 1 | 15 |
| 2 | 27 |
| 3 | 8 |
| 4 | 5 |
What is the mean number of Parking Spaces?
Answer:
The Mean is 2.05 (to 2 decimal places)
(much easier than adding all numbers separately!)
Notation
Now you know how to do it, let's do that last example again, but using formulas.
(read more at Sigma Notation)
(where f is frequency)
And we can use it like this:
![]()
Likewise we can add up "frequency times score" this way:
![]()
(where f is frequency and x is the matching score)
And the formula for calculating the mean from a frequency table is:
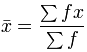
The x with the bar on top says "the mean of x"
So now we are ready to do our example above, but with correct notation.
Example: Calculate the Mean of this Frequency Table
| x | f |
|---|---|
| 1 | 15 |
| 2 | 27 |
| 3 | 8 |
| 4 | 5 |
And here it is:
There you go! You can use sigma notation.
Calculate in the Table
It is often better to do the calculations in the table.
Example: (continued)
From the previous example, calculate f × x in the right-hand column and then do totals:
| x | f | fx |
|---|---|---|
| 1 | 15 | 15 |
| 2 | 27 | 54 |
| 3 | 8 | 24 |
| 4 | 5 | 20 |
| TOTALS: | 55 | 113 |
And the Mean is then easy:
Mean of x = 11355 = 2.05...