Probability: Complement
Complement of an Event: All outcomes that are NOT the event.
 |
When the event is Heads, the complement is Tails |
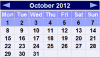 |
When the event is {Monday, Wednesday} the complement is {Tuesday, Thursday, Friday, Saturday, Sunday} |
 |
When the event is {Hearts} the complement is {Spades, Clubs, Diamonds, Jokers} |
So the Complement of an event is all the other outcomes (not the ones we want).
And together the Event and its Complement make all possible outcomes.
Probability
Probability of an event happening = Number of ways it can happenTotal number of outcomes
Example: the chances of rolling a "4" with a die
Number of ways it can happen: 1 (there is only 1 face with a "4" on it)
Total number of outcomes: 6 (there are 6 faces altogether)
So the probability = 16
The probability of an event is shown using "P":
P(A) means "Probability of Event A"
The complement is shown by a little mark after the letter such as A' (or sometimes Ac or A):
P(A') means "Probability of the complement of Event A"
The two probabilities always add to 1
P(A) + P(A') = 1
Example: Rolling a "5" or "6"
Event A is {5, 6}
Number of ways it can happen: 2
Total number of outcomes: 6
P(A) = 26 = 13
The Complement of Event A is {1, 2, 3, 4}
Number of ways it can happen: 4
Total number of outcomes: 6
P(A') = 4 6 = 2 3
Let us add them:
P(A) + P(A') = 1 3 + 2 3 = 3 3 = 1
Yep, that makes 1
It makes sense, right? Event A plus all outcomes that are not Event A make up all possible outcomes.
Why is the Complement Useful?
It is sometimes easier to work out the complement first.
Example. Throw two dice. What is the probability the two scores are different?
Different scores are like getting a 2 and 3, or a 6 and 1. It is a long list:
A = { (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), ... etc ! }
But the complement (which is when the two scores are the same) is only 6 outcomes:
A' = { (1,1), (2,2), (3,3), (4,4), (5,5), (6,6) }
And its probability is:
P(A') = 636 = 16
Knowing that P(A) and P(A') together make 1, we can calculate:
| P(A) | = 1 − P(A') |
| = 1 − 16 | |
| = 56 |
So in this case (and many others) it is easier to work out P(A') first, then calculate P(A) = 1 − P(A')
