What is Area?
Area is the size of a surface!
Example:
These shapes all have the same area of 9:
Area of Simple Shapes
There are special formulas for certain shapes:
Example: What is the area of this rectangle?
The formula is:
Area = w × h
w = width
h = height
The width is 5, and the height is 3, so we know w = 5 and h = 3. So:
Area = 5 × 3 = 15
Read Area of Plane Shapes for more information.
Area of Difficult Shapes
To help you understand an area, imagine painting it and how much paint you might use.
You can sometimes break a shape up into two or more simpler shapes:
Example: What is the area of this Shape?
Let's break the area into two parts:
Part A is a square:
Part B is a triangle. Viewed sideways it has a base of 20m and a height of 14m.
So the total area is:
Area by Adding Up Triangles
You can also break up a shape into triangles:
Then measure the base (b) and height (h) of each triangle:
Then calculate each area (using Area = ½b × h) and add them all up.
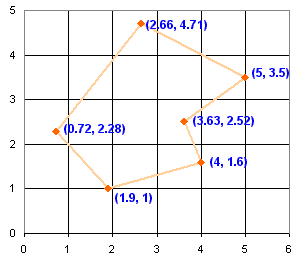
Area by CoordinatesIf you know the coordinates of each corner point you can use the method explained in Area of Irregular Polygons: There is an Area of a Polygon by Drawing Tool if you need it. |
 |
Area by Counting Squares
You can also put your shape on a grid and count the number of squares:
This rectangle has an area of 15
If each square was 1 cm on a side, then the area would be 15 cm2 (15 square cm)
Sometimes the squares may not match the shape exactly, so you will need to "approximate" an answer.
One way is:
- more than half a square counts as 1
- less than half a square counts as 0
Like this:
This pentagon has an area of approximately 17
Or just use your eyes and count a whole square when the areas seem to add up, like with this circle, where the area marked "4" seems equal to about 1 whole square (also for "8"):
This circle has an area of approximately 14