Interior Angles of Polygons

An Interior Angle is an angle inside a shape:

Another example:

Triangles

The Interior Angles of a Triangle add up to 180°

Let's try a triangle:

90° + 60° + 30° = 180°

It works for this triangle

Now tilt a line by 10°:

80° + 70° + 30° = 180°

It still works!
One angle went up by 10°,
and the other went down by 10°

Quadrilaterals (Squares, etc)

(A Quadrilateral has 4 straight sides)

The Interior Angles of a Quadrilateral add up to 360°

Because there are 2 triangles in a square ...

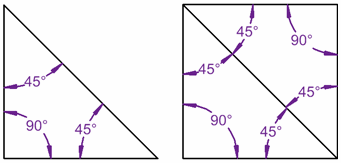
The interior angles in a triangle add up to 180° ...

... and for the square they add up to 360° ...

... because the square can be made from two triangles!

Pentagon

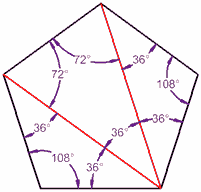
A pentagon has 5 sides, and can be made from three triangles, so you know what ...

... its interior angles add up to 3 × 180° = 540°

And when it is regular (all angles the same), then each angle is 540° / 5 = 108°

(Exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior angles add up to 540°)

The Interior Angles of a Pentagon add up to 540°

The General Rule

Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total:

			If it is a Regular Polygon (all sides are equal, all angles are equal)
Shape	Sides	Sum of Interior Angles	Shape	Each Angle
Triangle	3	180°		60°
Quadrilateral	4	360°		90°
Pentagon	5	540°		108°
Hexagon	6	720°		120°
Heptagon (or Septagon)	7	900°		128.57...°
Octagon	8	1080°		135°
Nonagon	9	1260°		140°
...	...	..	...	...
Any Polygon	n	(n−2) × 180°		(n−2) × 180° / n

So the general rule is:

Perhaps an example will help:

Example: What about a Regular Decagon (10 sides) ?

Sum of Interior Angles

= (n−2) × 180°

= (10−2) × 180°

= 8 × 180°

= 1440°

And for a Regular Decagon:

Each interior angle = 1440°/10 = 144°