Tessellation

A pattern of shapes that fit perfectly together!

A Tessellation (or Tiling) is when we cover a surface with a pattern of flat shapes so that there are no overlaps or gaps.

Examples:

Tessellation pattern made of rectangles
Rectangles
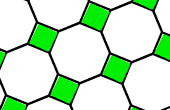
Tessellation pattern made of octagons and squares
Octagons and Squares
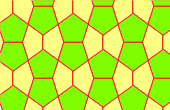
Tessellation pattern made of different, irregular pentagons
Different Pentagons

Regular Tessellations

A regular tessellation is a pattern made by repeating a regular polygon (which has all sides equal and angles equal).

There are only 3 regular tessellations:

Regular tessellation of equilateral triangles with vertex notation 3.3.3.3.3.3
Triangles
3.3.3.3.3.3
Regular tessellation of squares with vertex notation 4.4.4.4
Squares
4.4.4.4
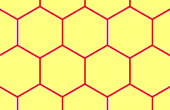
Regular tessellation of regular hexagons with vertex notation 6.6.6
Hexagons
6.6.6

Look at a Vertex ...

Magnified view of a tessellation vertex, showing shapes meeting at a point A vertex is a corner point.

What shapes meet here?

Three hexagons meet at this vertex.

Each hexagon has 6 sides

So this gets called a "6.6.6" tessellation.

 Vertex of a hexagonal tessellation illustrating 6.6.6 notation

Why Only 3 Regular Tessellations?

For shapes to fit perfectly at a vertex their angles must add up to exactly 360°.

Let's test the first few:

Polygon Interior Angle How to get 360° Fits?
Triangle 60° 60° × 6 = 360° YES
Square 90° 90° × 4 = 360° YES
Pentagon 108° 108° × 3.33... NO (Gap)
Hexagon 120° 120° × 3 = 360° YES
Heptagon ~128.6° 128.6° × 2.8... NO (Overlap)
Octagon 135° 135° × 2.6... NO (Overlap)

Any shape with more than 6 sides has angles too large to fit 3 or more around a point without overlapping!

Semi-Regular Tessellations

A semi-regular tessellation is made of two or more regular polygons. The pattern at each vertex must be the same!

There are only 8 semi-regular tessellations:

Semi-regular tessellation with vertex notation 3.3.3.3.6 (triangles and hexagons)
3.3.3.3.6
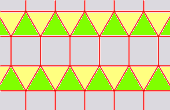
Semi-regular tessellation with vertex notation 3.3.3.4.4 (triangles and squares)
3.3.3.4.4
Semi-regular tessellation with vertex notation 3.3.4.3.4 (triangles and squares)
3.3.4.3.4
Semi-regular tessellation with vertex notation 3.4.6.4 (triangles, squares, and hexagons)
3.4.6.4
Semi-regular tessellation with vertex notation 3.6.3.6 (triangles and hexagons)
3.6.3.6
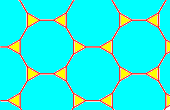
Semi-regular tessellation with vertex notation 3.12.12 (triangles and dodecagons)
3.12.12
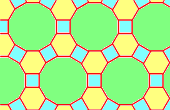
Semi-regular tessellation with vertex notation 4.6.12 (squares, hexagons, and dodecagons)
4.6.12
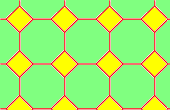
Semi-regular tessellation with vertex notation 4.8.8 (squares and octagons)
4.8.8

Naming

To name a tessellation, go around a vertex and write down how many sides each polygon has, in order, like "3.12.12".

And always start at the polygon with the least number of sides, so "3.12.12", not "12.3.12"

Question mark icon Question 1: For all the tessellations above, is the pattern the same at each vertex?
Question mark icon Question 2: One of those patterns becomes different when we make a mirror-image of it ... which one?

Other Tessellations

There are also "demiregular" tessellations, but mathematicians disagree on what they actually are!

And some people allow curved shapes (not just polygons) so we can have tessellations like these:

Tessellation pattern made of curvy, irregular shapes
Curvy Shapes
Tessellation pattern combining circles and lines
Circles
Tessellation pattern made of stylized eagle shapes
Eagles?

Tessellation Artist

All these images were made using Tessellation Artist, with some color added using a paint program.

You can try it too - maybe you will invent a new tessellation!

Graphic of celebratory balloons

World Tessellation Day

World Tessellation Day is June 17. Celebrate!

5482, 5483, 5484, 5485, 5486, 853, 854, 3368, 3369, 5487
Tessellation Artist Symmetry Artist Geometry Index