3, 4, 5 Triangle
Need a Right Angle (90°) Fast ... ?
Make a 3,4,5 Triangle!
- 3 long
- 4 long
- 5 long
And you will have a right angle (90°)
Other Lengths
You can use other lengths by multiplying each side by 2. Or by 10. Or any multiple.
Drawing It
Let us say you need to mark a right angle coming from a point on a wall.
You decide to use 300, 400 and 500 cm lines.
 |
 |
 |
 |
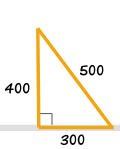 |
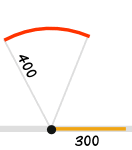
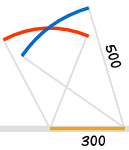
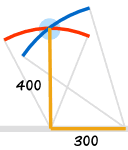
| Draw a 300 line along the wall | Draw an arc 400 away from the start of the 300 line | Draw an arc 500 away from the end of the 300 line | Connect from the start of the 300 line to where the arcs cross | And you have your "3,4,5" triangle with its right angle |
The Mathematics Behind It
The Pythagoras Theorem says:
|
In a right-angled triangle, the square of a (a2) plus the square of b (b2) is equal to the square of c (c2): a2 + b2 = c2 |
Let's check if it does work: 32 + 42 = 52 Calculating this becomes: 9 + 16 = 25 Yes, it works ! |

Other Combinations
Yes, there are other combinations that work (not just by multiplying). Here are two others:
| 5,12,13 triangle | 9,40,41 Triangle | |
| 52 + 122 = 132 | 92 + 402 = 412 | |
| 25 + 144 = 169 | (try it yourself) |
And there are infinitely many more.... read Pythagorean Triples for more information.
But Wait ... There is More!
The 3,4,5 Triangle has a simple beauty. At its heart is a circle:
The circle is a Unit Circle: it has a radius of exactly 1 and an area of π
And using that circle we can cut our triangle into six little triangles like this:
Each small triangle is also a right triangle!
And notice that 1+2=3, 1+3=4 and 2+3=5, making the 3,4,5 triangle. So simple and neat.
Is the Radius Really 1?
Imagine we don't know the radius, call it "r" and draw in what we do know: