Sine, Cosine and Tangent

Three Functions, but same idea.

Right Triangle

Sine, Cosine and Tangent are all based on a Right-Angled Triangle

Before getting stuck into the functions, it helps to give a name to each side of a right triangle:

triangle showing Opposite, Adjacent and Hypotenuse

"Opposite" is opposite to the angle θ
"Adjacent" is adjacent (next to) to the angle θ
"Hypotenuse" is the long one

Adjacent is always next to the angle

And Opposite is opposite the angle

Sine, Cosine and Tangent

Sine, Cosine and Tangent are the three main functions in trigonometry.

They are often shortened to sin, cos and tan.

To calculate them:

Divide the length of one side by another side
... but you must know which sides!

For a triangle with an angle θ, the functions are calculated this way:

Sine Function:	sin(θ) = Opposite / Hypotenuse
Cosine Function:	cos(θ) = Adjacent / Hypotenuse
Tangent Function:	tan(θ) = Opposite / Adjacent

In picture form:

Example: What is the sine of 35°?

Using this triangle (lengths are only to one decimal place):

sin(35°) = Opposite / Hypotenuse = 2.8 / 4.9 = 0.57...

How to remember? Think "Sohcahtoa"! It works like this:

*Soh...*	Sine = Opposite / Hypotenuse
*...cah...*	Cosine = Adjacent / Hypotenuse
*...toa*	Tangent = Opposite / Adjacent

You can read more about sohcahtoa ... please remember it, it may help in an exam !

View Larger

Try It!

Have a try! Drag the corner around to see how different angles (in radians or degrees) affect sine, cosine and tangent.

In this animation the hypotenuse is 1, making the Unit Circle.

Notice that the adjacent side and opposite side can be positive or negative, which makes the sine, cosine and tangent change between positive and negative values also.

Good calculators have sin, cos and tan on them, to make it easy for you. Just put in the angle and press the button.

But you still need to remember what they mean!

"Why didn't sin and
tan go to the party?"
"... just cos!"

Examples

Example: what are the sine, cosine and tangent of 30° ?

The classic 30° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of √(3):

30° triangle

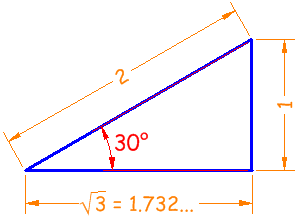
Now we know the lengths, we can calculate the functions:

Sine	sin(30°) = 1 / 2 = 0.5
Cosine	cos(30°) = 1.732 / 2 = 0.866...
Tangent	tan(30°) = 1 / 1.732 = 0.577...

(get your calculator out and check them!)

Example: what are the sine, cosine and tangent of 45° ?

The classic 45° triangle has two sides of 1 and a hypotenuse of √(2):

45° triangle

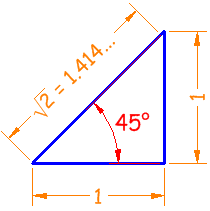
Sine	sin(45°) = 1 / 1.414 = 0.707...
Cosine	cos(45°) = 1 / 1.414 = 0.707...
Tangent	tan(45°) = 1 / 1 = 1

Why?

Why are these functions important?

Because they let you work out angles when you know sides
And they let you work out sides when you know angles

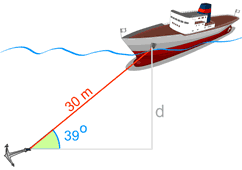
Example: Use the sine function to find "d"

We know

* The angle the cable makes with the seabed is 39°

* The cable's length is 30 m.

And we want to know "d" (the distance down).

Start with:		sin 39° = opposite/hypotenuse = d/30
Swap Sides:		d/30 = sin 39°
Use a calculator to find sin 39°:		d/30 = 0.6293…
Multiply both sides by 30:		d = 0.6293… x 30 = 18.88 to 2 decimal places.

The depth "d" is 18.88 m

Exercise

Try this paper-based exercise where you can calculate the sine function for all angles from 0° to 360°, and then graph the result. It will help you to understand these relatively simple functions.

You can also see Graphs of Sine, Cosine and Tangent.

Less Common Functions

To complete the picture, there are 3 other functions where you divide one side by another, but they are not so commonly used.

They are equal to 1 divided by cos, 1 divided by sin, and 1 divided by tan:

Secant Function:	sec(θ) = Hypotenuse / Adjacent	(=1/cos)
Cosecant Function:	csc(θ) = Hypotenuse / Opposite	(=1/sin)
Cotangent Function:	cot(θ) = Adjacent / Opposite	(=1/tan)