Graphing Quadratic Equations

A Quadratic Equation in Standard Form
(a, b, and c can have any value, except that a can't be 0.)

Here is an example:

Quadratic Equation

Graphing

You can graph a Quadratic Equation using the Function Grapher, but to really understand what is going on, you can make the graph yourself. Read On!

The Simplest Quadratic

The simplest Quadratic Equation is:

f(x) = x²

And its graph is simple too:

Square function

This is the curve f(x) = x²
It is a parabola.

Now let us see what happens when we introduce the "a" value:

f(x) = ax²

ax^2

Larger values of a squash the curve inwards
Smaller values of a expand it outwards
And negative values of a flip it upside down

Play With It

Now is a good time to play with the
"Quadratic Equation Explorer" so you can
see what different values of a, b and c do.

The "General" Quadratic

Before graphing we rearrange the equation, from this:

f(x) = ax² + bx + c

To this:

f(x) = a(x-h)² + k

Where:

h = −b/2a
k = f( h )

In other words, calculate h (= −b/2a), then find k by calculating the whole equation for x=h

But Why?

quadratic vertex

The wonderful thing about this new form is that h and k show us the very lowest (or very highest) point, called the vertex:

And also the curve is symmetrical (mirror image) about the axis that passes through x=h, making it easy to graph

So ...

h shows us how far left (or right) the curve has been shifted from x=0
k shows us how far up (or down) the curve has been shifted from y=0

Lets see an example of how to do this:

Example: Plot f(x) = 2x² − 12x + 16

First, let's note down:

a = 2,
b = −12, and
c = 16

Now, what do we know?

a is positive, so it is an "upwards" graph ("U" shaped)
a is 2, so it is a little "squashed" compared to the x²graph

Next, let's calculate h:

h = −b/2a = −(−12)/(2x2) = 3

And next we can calculate k (using h=3):

k = f(3) = 2(3)² − 12·3 + 16 = 18−36+16 = −2

So now we can plot the graph (with real understanding!):

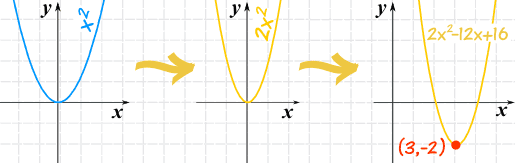
2x^2-12x+16

We also know: the vertex is (3,−2), and the axis is x=3

From A Graph to The Equation

What if we have a graph, and want to find an equation?

Example: you have just plotted some interesting data, and it looks Quadratic:

quadratic data

Just knowing those two points we can come up with an equation.

Firstly, we know h and k (at the vertex):

(h, k) = (1, 1)

So let's put that into this form of the equation:

f(x) = a(x-h)² + k

f(x) = a(x−1)² + 1

Then we calculate "a":

We know the point (0, 1.5) so:f(0) = 1.5

And a(x−1)² + 1 at x=0 is:f(0) = a(0−1)² + 1

They are both f(0) so make them equal: a(0−1)² + 1 = 1.5

Simplify:a + 1 = 1.5

a = 0.5

And here is the resulting Quadratic Equation:

f(x) = 0.5(x−1)² + 1

Note: This may not be the correct equation for the data, but it’s a good model and the best we can come up with.

567,7335,7336,7337,7338,1207,2443,2444,2445,2447