Rotational Symmetry

Rotational Symmetry

A shape has Rotational Symmetry when it still looks exactly the same after some rotation less than one full turn.

As we go all the way around once (a full turn), we can count how many times it matches itself. This number is called the Order of rotational symmetry.

How many times it matches as we go once around is called the Order.

Think of propeller blades (like below). When we turn the propeller around its center, it keeps looking the same again and again.

Examples of Different Rotational Symmetry Order

Order	Example Shape	Artwork
		(using Symmetry Artist)
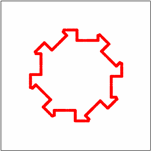
... and there is also Order 5, 6, 7, and ...
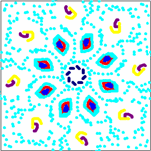... and Orders 9, 10, and so on.

Try rotational symmetry yourself with Symmetry Artist ... !

Is there Rotational Symmetry of Order 1 ?

Not really! If a shape only matches itself once as we go around (ie it matches itself after one full rotation) there is really no symmetry at all ...

... because the word "Symmetry" comes from syn- together and metron measure, and there can't be "together" if there is just one thing.

Angles

We can calculate the angle of each turn! Take the full rotation of 360° and divide by the order n:

Angle of Each Turn = 360°n

Example: Order 4

Angle of Each Turn = 360°4 = 90°

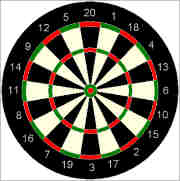
Real World Examples

A Dartboard has Rotational Symmetry of Order 10	The US Bronze Star Medal has Order 5	The London Eye has Order ... oops, I lost count!