Squares and Square Roots

How to Square A Number

Example: What is 3 squared?

3 Squared

=

= 3 × 3 = 9

"Squared" is often written as a little 2 like this:

This says "4 Squared equals 16"
(the little 2 says the number appears twice in multiplying)

Squares From 1² to 6²

You can also find the squares on the Multiplication Table:

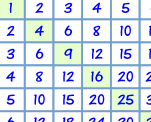Negative Numbers

You can also square negative numbers.

That was interesting!

When you square a negative number you get a positive result.

Just the same as if you had squared a positive number:

We look at that in more detail in Squares and Square Roots in Algebra.

Square Roots

A square root goes the other way:

3 squared is 9, so a square root of 9 is 3

A square root of a number is ...

A square root of 9 is ...

It is like asking:

Note: When you see "root" think "I know the tree, but what is the root that produced it?" In this case the tree is "9", and the root is "3".

Here are some more squares and square roots:

4		16
5		25
6		36

Decimal Numbers

You can also square decimal numbers.

Try the sliders below. Note: the numbers here are only shown to 2 decimal places.

Using the sliders (remembering it is only accurate to 2 decimal places):

• What is the square root of 8?
• What is the square root of 9?
• What is the square root of 10?
• What is 1 squared?
• What is 1.1 squared?
• What is 2.6 squared?

The Square Root Symbol

This is the special symbol that means "square root", it is sort of like a tick, and actually started hundreds of years ago as a dot with a flick upwards. It is called the radical, and always makes math look important!

You can use it like this:

you would say "square root of 9 equals 3"

Perfect Squares

The perfect squares are the squares of the whole numbers:

Try to remember at least the first 10 of those.

Calculating Square Roots

It is easy to work out the square root of a perfect square, but it is really hard to work out other square roots.

Example: what is √10?

Well, 3 × 3 = 9 and 4 × 4 = 16, so we can guess the answer is between 3 and 4.

• Let's try 3.5: 3.5 × 3.5 = 12.25
• Let's try 3.2: 3.2 × 3.2 = 10.24
• Let's try 3.1: 3.1 × 3.1 = 9.61
• ...

Getting closer to 10, but it will take a long time to get a good answer!

 

At this point, I get out my calculator and it says: 3.1622776601683793319988935444327 But the digits just go on and on, without any pattern. So even the calculator's answer is only an approximation !

Note: numbers like that are called Irrational Numbers, if you want to know more.

The Easiest Way to Calculate a Square Root

Use your calculator's square root button!

And also use your common sense to make sure you have the right answer.

A Fun Way to Calculate a Square Root

There is a fun method for calculating a square root that gets more and more accurate each time around:

	a) start with a guess (let's guess 4 is the square root of 10)
	b) divide by the guess (10/4 = 2.5) c) add that to the guess (4 + 2.5 = 6.5) d) then divide that result by 2, in other words halve it. (6.5/2 = 3.25) e) now, set that as the new guess, and start at b) again

• Our first attempt got us from 4 to 3.25
  
• Going again (b to e) gets us: 3.163
  
• Going again (b to e) gets us: 3.1623

And so, after 3 times around the answer is 3.1623, which is pretty good, because:

3.1623 x 3.1623 = 10.00014

Now ... why don't you try calculating the square root of 2 this way?

How to Guess

What if you have to guess the square root for a difficult number such as "82,163" ... ?

In that case I would think to myself "82,163" has 5 digits, so the square root might have 3 digits (100x100=10,000), and the square root of 8 (the first digit) is about 3 (3x3=9), so 300 would be a good start.