Working with Exponents and Logarithms

What is an Exponent?

The exponent of a number says how many times
to use the number in a multiplication.

In this example: 2³ = 2 × 2 × 2 = 8

(2 is used 3 times in a multiplication to get 8)

What is a Logarithm?

A Logarithm goes the other way.

It asks the question "what exponent produced this?":

Logarithm Question

And answers it like this:

exponent to logarithm

In that example:

The Exponent takes 2 and 3 and gives 8 (2, used 3 times in a multiplication, makes 8)
The Logarithm takes 2 and 8 and gives 3 (2 makes 8 when used 3 times in a multiplication)

A Logarithm says how many of one number to multiply to get another number

So a logarithm actually gives us the exponent as its answer:

logarithm concept

(Also see how Exponents, Roots and Logarithms are related.)

Working Together

Exponents and Logarithms work well together because they "undo" each other (so long as the base "a" is the same):

Exponent vs Logarithm

They are "Inverse Functions"

Doing one, then the other, gets us back to where we started:

Doing a^x then log_a gives us back x:log_a(a^x) = x

Doing log_a then a^x gives us back x:a^log_a(x) = x

It is too bad they are written so differently ... it makes things look strange. So it may help to think of a^x as "up" and log_a(x) as "down":

going up then down returns us back again:down(up(x)) = x

going down then up returns us back again:up(down(x)) = x

Anyway, the important thing is that:

The Logarithmic Function is "undone" by the Exponential Function.

(and vice versa)

Like in this example:

Example, what is x in log₃(x) = 5

We want to "undo" the log₃ so we can get "x ="

Start with:log₃(x) = 5

Use the Exponential Function on both sides:3^log₃(x) = 3⁵

And we know that 3^log₃(x) = x, so:x = 3⁵

Answer: x = 243

And also:

Example: Calculate y in y = log₄(14)

Start with:y = log₄(14)

Use the Exponential Function on both sides:4^y = 4^log₄(14)

Simplify:4^y = 14

Now a simple trick: 14 = 4^-1

So:4^y = 4^-1

And so:y = −1

Properties of Logarithms

One of the powerful things about Logarithms is that they can turn multiply into add.

log_a( m × n ) = log_am + log_an

"the log of multiplication is the sum of the logs"

Why is that true? See Footnote.

Using that property and the Laws of Exponents we get these useful properties:

the log of multiply is the sum of the logs:

log_a(m × n) = log_am + log_an

the log of divide is the difference of the logs:

log_a(m/n) = log_am − log_an

that division rule also gets us:

log_a(1/n) = −log_an as log_a(1) = 0

the log of m with an exponent r is r times the log of m:

log_a(m^r) = r ( log_am )

Remember: the base "a" is always the same!

book of logarithms History: Logarithms were very useful before calculators were invented ... for example, instead of multiplying two large numbers, by using logarithms we can turn it into addition (much easier!)

And there were books full of Logarithm tables to help.

Let us have some fun using the properties:

Example: Simplify log_a( (x²+1)⁴√x )

Start with:log_a( (x²+1)⁴√x )

Use log_a(mn) = log_am + log_an:log_a( (x²+1)⁴ ) + log_a( √x )

Use log_a(m^r) = r ( log_am ): 4 log_a(x²+1) + log_a( √x )

Also √x = x^½:4 log_a(x²+1) + log_a( x^½ )

Use log_a(m^r) = r ( log_am ) again: 4 log_a(x²+1) + ½ log_a(x)

That is as far as we can simplify it ... we can't do anything with log_a(x²+1)

Answer: 4 log_a(x²+1) + ½ log_a(x)

Note: there is no rule for handling log_a(m+n) or log_a(m−n)

We can also apply the logarithm rules "backwards" to combine logarithms:

Example: Turn this into one logarithm: log_a(5) + log_a(x) − log_a(2)

Start with:log_a(5) + log_a(x) − log_a(2)

Use log_a(mn) = log_am + log_an:log_a(5x) − log_a(2)

Use log_a(m/n) = log_am − log_an: log_a(5x/2)

Answer: log_a(5x/2)

The Natural Logarithm and Natural Exponential Functions

When the base is Euler's Number e = 2.718281828459... we get:

The Natural Logarithm log_e(x) which is more commonly written ln(x)
The Natural Exponential Function e^x

And the same idea that one can "undo" the other is still true:

ln(e^x) = x

e^{(ln x)} = x

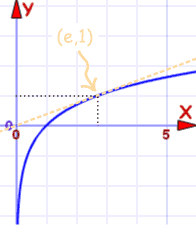
And here are their graphs:

Natural Logarithm		Natural Exponential Function

Graph of f(x) = ln(x)		Graph of f(x) = e^x
Passes through (1,0) and (e,1)		Passes through (0,1) and (1,e)

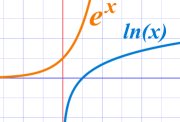
ln(x) vs e^x

They are the same curve with x-axis and y-axis flipped.

Which is another thing showing us they are inverse functions.

On a calculator the Natural Logarithm is the "ln" button.

Always try to use Natural Logarithms and the Natural Exponential Function whenever possible.

The Common Logarithm

When the base is 10 we get:

The Common Logarithm log₁₀(x), which is sometimes written as log(x)

Engineers love to use it, but it is not used much in mathematics.

On a calculator the Common Logarithm is the "log" button.

It is handy because it tells us how "big" the number is in decimal (how many times we need to use 10 in a multiplication).

Example: Calculate log₁₀ 100

Well, 10 × 10 = 100, so when 10 is used 2 times in a multiplication we get 100:

log₁₀ 100 = 2

Likewise log₁₀ 1,000 = 3, log₁₀ 10,000 = 4, and so on.

Example: Calculate log₁₀ 369

OK, best to use my calculator's "log" button:

log₁₀ 369 = 2.567...

Changing the Base

What if we want to change the base of a logarithm?

We can use this formula:

Log Change Base

"x goes up, a goes down"

1log_b a works as a "conversion factor" from one base to any other base.

Another useful property is:

log_a x = 1 / log_x a

Log Reciprocal

See how "x" and "a" swap positions?

Example: Calculate 1 / log₈ 2

1 / log₈ 2 = log₂ 8

And 2 × 2 × 2 = 8, so when 2 is used 3 times in a multiplication we get 8:

1 / log₈ 2 = log₂ 8 = 3

And we use the Natural Logarithm so often it is worth remembering this:

log_a x = ln x / ln a

Example: Calculate log₄ 22

My calculator doesn't have a "log₄" button ...

... but it does have an "ln" button, so we can use that:

log₄ 22 = ln 22 / ln 4

= 3.09... / 1.39...

= 2.23 (to 2 decimal places)

What does this answer mean? It means that 4 with an exponent of 2.23 equals 22. So we can check that answer:

Check: 4^2.23 = 22.01 (close enough!)

Here is another example:

Example: Calculate log₅ 125

We can use the "ln" function on the calculator:

log₅ 125 = ln 125 / ln 5

= 4.83... / 1.61...

=3.00 (to 2 decimal places)

Is it exactly 3? We should not trust a calculator as there could be rounding errors, but in this case we can check that 5³ = 5 × 5 × 5 = 125 exactly, so:

Answer: 3

Real World Usage

Here are some uses for Logarithms in the real world:

Earthquakes

The magnitude of an earthquake is a Logarithmic scale.

The famous "Richter Scale" uses this formula:

M = log₁₀ A + B

Where A is the amplitude (in mm) measured by the Seismograph
and B is a distance correction factor

Nowadays there are more complicated formulas, but they still use a logarithmic scale.

Sound

Loudness is measured in Decibels (dB for short):

Loudness in dB = 10 log₁₀ (p × 10¹²)

where p is the sound pressure.

Acidic or Alkaline

Acidity (or Alkalinity) is measured in pH:

pH = −log₁₀ [H⁺]

where H⁺ is the molar concentration of dissolved hydrogen ions.
Note: in chemistry [ ] means molar concentration (moles per liter).

More Examples

Example: Solve 2 log₈ x = log₈ 16

Start with:2 log₈ x = log₈ 16

Bring the "2" into the log:log₈ x² = log₈ 16

Remove the logs (they are same base): x² = 16

Solve:x = −4 or +4

But ... but ... but ... we can't have a log of a negative number!

So the −4 case is not defined.

Answer: 4

Check: use a calculator to see if this is the right answer ... also try the "−4" case.

Example: Solve e^−w = e^2w+6

Start with:e^-w = e^2w+6

Apply ln to both sides:ln(e^-w) = ln(e^2w+6)

And ln(e^w)=w: −w = 2w+6

Simplify:−3w = 6

Solve:w = 6/−3 = −2

Answer: w = −2

Check: e^-(−2) = e² and e^2(−2)+6 = e²

Footnote: Why does log(m × n) = log(m) + log(n) ?

To see why, we will use a^log_a(x) = x and log_a(a^x) = x like this:

Log Product Rule

So we seem to make things more complicated by transforming into a^log_a(x)but then we are able to add them, then we transform back again and we have a solution!

It is one of those clever things we do in mathematics which can be described as "we can't do it here, so let's go over there, do it, then come back".

585, 1234, 587, 1237, 8137, 8221, 8243, 8244, 8138, 8222