Geometric Sequences and Sums
Sequence
A Sequence is a set of things (usually numbers) that are in order.
 |
Geometric Sequences
In a Geometric Sequence each term is found by multiplying the previous term by a constant.
Example:
| 2, 4, 8, 16, 32, 64, 128, 256, ... |
This sequence has a factor of 2 between each number.
Each term (except the first term) is found by multiplying the previous term by 2.
In General you could write a Geometric Sequence like this:
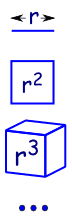
{a, ar, ar2, ar3, ... }
where:
- a is the first term, and
- r is the factor between the terms (called the "common ratio")
Example: {1,2,4,8,...}
The sequence starts at 1 and doubles each time, so
- a=1 (the first term)
- r=2 (the "common ratio" between terms is a doubling)
So we would get:
{a, ar, ar2, ar3, ... }
= {1, 1×2, 1×22, 1×23, ... }
= {1, 2, 4, 8, ... }
But be careful, r should not be 0:
- When r=0, you get the sequence {a,0,0,...} which is not geometric
The Rule
You can also calculate any term using the Rule:
xn = ar(n-1)
(We use "n-1" because ar0 is for the 1st term)
Example:
| 10, 30, 90, 270, 810, 2430, ... |
This sequence has a factor of 3 between each number.
The values of a and r are:
- a = 10 (the first term)
- r = 3 (the "common ratio")
The Rule for any term is:
xn = 10 × 3(n-1)
So, the 4th term would be:
x4 = 10×3(4-1) = 10×33 = 10×27 = 270
And the 10th term would be:
x10 = 10×3(10-1) = 10×39 = 10×19683 = 196830
A Geometric Sequence can also have smaller and smaller values:
Example:
| 4, 2, 1, 0.5, 0.25, ... |
This sequence has a factor of 0.5 (a half) between each number.
Its Rule is xn = 4 × (0.5)n-1
Why "Geometric" Sequence?
Because it is like increasing the dimensions in geometry:
 |
a line is 1-dimensional and has a length of r |
| in 2 dimensions a square has an area of r2 | |
| in 3 dimensions a cube has volume r3 | |
| etc (yes you can have 4 and more dimensions in mathematics). |
Geometric Sequences are sometimes called Geometric Progressions (G.P.’s)
Summing a Geometric Series
When you need to sum a Geometric Sequence, there is a handy formula.
To sum:
a + ar + ar2 + ... + ar(n-1)
Each term is ark, where k starts at 0 and goes up to n-1
Use this formula:
a is the first term
r is the "common ratio" between terms
n is the number of terms
What is that funny symbol? It is called Sigma Notation
 |
(called Sigma) means "sum up" |
And below and above it are shown the starting and ending values:
It says "Sum up n where n goes from 1 to 4. Answer=10
The formula is easy to use ... just "plug in" the values of a, r and n
Example: Sum the first 4 terms of
| 10, 30, 90, 270, 810, 2430, ... |
This sequence has a factor of 3 between each number.
The values of a, r and n are:
- a = 10 (the first term)
- r = 3 (the "common ratio")
- n = 4 (we want to sum the first 4 terms)
So:
Becomes:
You could check it yourself:
10 + 30 + 90 + 270 = 400
And, yes, it was easier to just add them in this case, because there were only 4 terms. But imagine you had to sum up lots of terms, then the formula is better to use.
Using the Formula
Let's see the formula in action:
Example: Grains of Rice on a Chess Board
 |
On our page Binary Digits we give an example of grains of rice on a chess board. The question is asked: When you place rice on the chess board:
... doubling the grains of rice on each square ... ... how many grains of rice in total? |
So we have:
- a = 1 (the first term)
- r = 2 (doubles each time)
- n = 64 (64 squares on a chess board)
So:
Becomes:
= (1-264) / (-1) = 264 - 1
= 18,446,744,073,709,551,615
Which was exactly the result we got on the Binary Digits page (thank goodness!)
And another example, this time with r less than 1:
Example: Add up the first 10 terms of the Geometric Sequence that halves each time:
{ 1/2, 1/4, 1/8, 1/16, ... }
The values of a, r and n are:
- a = ½ (the first term)
- r = ½ (halves each time)
- n = 64 (10 terms to add)
So:
Becomes:
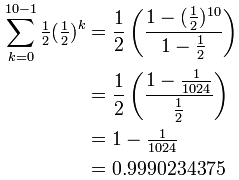
Very close to 1.
(Question: if we continue to increase n, what would happen?)
Why Does the Formula Work?
I want to show you why the formula works, because we get to use an interesting "trick" which is worth knowing.
| First, we will call the whole sum "S": | S = a + ar + ar2 + ... + ar(n-2)+ ar(n-1) | |
| Next, multiply S by r: | S·r = ar + ar2 + ar3 + ... + ar(n-1) + arn |
Notice that S and S·r are similar?
Now subtract them!
Wow! All the terms in the middle neatly cancel out.
(That is the neat trick I wanted to show you.)
By subtracting S·r from S we get a simple result:
S - S·r = a - arn
Let's rearrange it to find S:
| Factor out S and a: | S(1- r) = a(1- rn) | |
| Divide by (1-r): | S = a(1- rn)/(1- r) |
Which is our formula (ta-da!):
Infinite Geometric Series
So what happens when n goes to infinity?
Well ... when r is less than 1, then rn goes to zero and we get:
NOTE: this does not work when r is 1 or more (or less than -1):
r must be between (but not including) -1 and 1
and r should not be 0 because you get the sequence {a,0,0,...} which is not geometric
Let's bring back our previous example, and see what happens:
Example: Add up ALL the terms of the Geometric Sequence that halves each time:
{ 1/2, 1/4, 1/8, 1/16, ... }
We have:
- a = 1/2 (the first term)
- r = 1/2 (halves each time)
And so:
= ½ × 1 / ½ = 1
Yes ... adding (1/2)+(1/4)+(1/8)+... equals exactly 1.
Don't believe me? Just look at this square: By adding up (1/2)+(1/4)+(1/8)+... ... you end up with the whole thing! |
 |
Recurring Decimal
On another page we asked "Does 0.999... equal 1?", well, let us see if we can calculate it:
Example: Calculate 0.999...
We can write a recurring decimal as a sum like this:
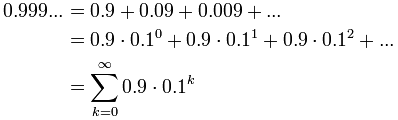
And now we can use the formula:
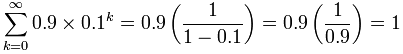
Yes! 0.999... does equal 1.
So there you have it ... Geometric Sequences (and their sums) can do all sorts of amazing and powerful things.