Electric Charge Calculations
Electric charge is a property of matter where it experiences a force when in an electromagnetic field.

The idea behind it is:
Fundamental particles can have 0, +1 or −1 electric charge:
- + and − are pulled towards each other
- + pushes + away
- − pushes − away
We sum it up by saying:
opposites attract and like charges repel
Charge is measured in Coulombs (C) and can be any multiple of the elementary charge (e), such as 0, +1e, −1e, +2e, −2e, and so on.
- e = 1.602176634 × 10-19 Coulombs. So small!
- A Coulomb equals the charge of about 6.241509×1018 electrons. That is a lot!
Electrons have a charge of −1e and protons have a charge of +1e
Electric charge can be felt far away (called an electric field).
In fact there is no limit, but it does get weaker the further we go.
Electric charge is conserved: it is neither created nor destroyed but can be transferred from one object to another.
A flow of electricity is called current because it is similar to a current of water:

There are other similarities to water, see Electricity Water Analogy for more.
Coulomb's law
Charge causes Force.
But how much force is there between two electrons? Not much really, and it depends on the distance between them
It is all given by Coulomb's law:
F = k q1q2r2
- F = Force between particles in Newtons (N)
- k = Coulombs' Constant (8.9875517873681764 x 109 Nm2/C2, or more simply 9 x 109)
- q1 and q2 = the charge of each particle in Coulombs (C)
- r = distance (m)
The bigger either of the charges the more force there is, but the force decreases by the square of the distance.
Example: Two electrons 1 mm Apart
The charge of a single electron is only about −1.6 x 10-19 Coulombs, let's use that for both q1 and q2 in Coulomb's Law:
Wow, that is small.
But there are a LOT of electrons in a piece of wire. A typical one meter wire has nearly 1023 atoms, most with a mobile electron.
Fun fact: Coulomb's law is very similar to the Law of Gravity:
Both calculate a force, have two items, get smaller by the square of the distance ... why is this?
Electric Fields
We can see the forces between charged particles using electric field diagrams (see Electric Chirps andElectric Field Animation for more)
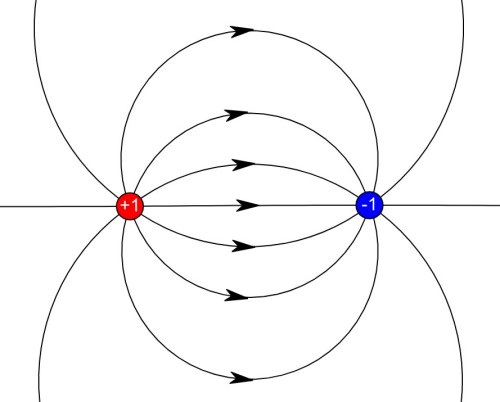
An electric field diagram
Anywhere in that electric field we have a field strength. It is measured in how many Newtons of force a Coulomb of charge feels: N/C
As we saw earlier there is very little force between just two charged particles, but a Coulomb of charge (about 6.241509×1018) changes the game entirely!
The force (F) felt by a charged particle in an electric field is calculated using:
F = qE
- F = Force on the charged particle (N)
- q = the object's charge in Coulombs (C)
- E = strength of the electric field (N/C)
Example: Calculating the Force on a Proton in an Electric Field
Suppose we have a uniform electric field with a strength of 500 N/C, directed upward, and we want to discover the force exerted on a single proton placed in this field. We know that the charge of a proton is approximately +1.602 x 10-19 Coulombs.
The positive sign of the force indicates that its direction is the same as the electric field, which in this case is upwards.
In the fun "Millikan oil drop experiment" you can watch oil droplets dance in the air, their movement controlled by the voltage applied. Remarkably, some droplets carry just a single electric charge.
Millikan used this experiment to calculate the electron's charge.
Calculating Work Done on a Charge by an Electric Field
For that electric charge to move around in the electric field requires Work. Either work gets done when the charge is pushed around, or the particle does work moving against the field.
Work is force by distance, so we take F = qE and include distance to get:
W = qEd
- W = Work done on point charge
- q = point charge in Coulombs (C)
- E = Electric field strength (V/m)
- d = distance between points parallel to field (m)
It calculates the work done W by or against an electric field E when a charge q moves a distance d forward or backward of that field.
Example: A particle with a positive charge of 2.0 x 10-19 Coulombs moves through a uniform electric field of 150 N/C. How much work is done by the electric field on the particle as it moves 0.05 meters?
It looks like this:
This amount of work would change the particle's kinetic energy, assuming no other forces act on the particle.
Work and energy are cornerstones of physics that describe the capability to perform actions, and in our electric world, charges moving through fields are a prime example of this principle in action.
This concept is fundamental in understanding how energy is stored in electric fields, such as in capacitors.
Capacitors store energy in an electric field. They are used in many applications, from stabilizing voltage and power flow, to sensing touch in touch-sensitive screens.
A simple parallel-plate capacitor:
Capacitor Diagram
In 3D it looks like this:
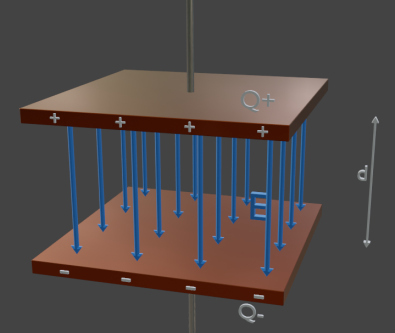
Capacitor Diagram in 3D
Voltage
Voltage V is like the electric "pressure" at a point in space, and it's what pushes electric charges around.
The voltage difference between two points can be calculated by:
V = Ed
- V = Voltage difference (V or J/C)
- E = Electric field strength (V/m)
- d = distance between points parallel to field (m)
Voltage from Work Done on a Charged Particle
V = W/q
- V = Voltage (V or J/C)
- W = Work done (J)
- q = the object charge in Coulombs (C)
Example: We have used 4.0 x 10-18 Joules (J) to push an electron through an electric field. What is the change in Voltage?
The charge of an electron, q, is -1.602 x 10-19 Coulombs (C). (Note that the charge of an electron is negative, but for this formula, we consider the magnitude of the charge).
This concept is key in understanding how batteries work. A battery's voltage tells us how much work per unit charge the battery can do to move electrons through a circuit. Higher voltage means more work can be done on each electron, which can result in a higher potential for doing electrical work.
Electric Field Strength from Voltage and Distance
We can rearrange V = Ed into this:
- E = Electric field strength (V/m)
- V = Voltage (V or J/C)
- d = distance between points parallel to field (m)
The negative sign in the formula accounts for the direction of the electric field, which is from higher to lower potential.
Example: Calculating Electric Field Strength from Voltage and Distance
Two parallel metal plates create a uniform electric field between them. The voltage, V, between the plates is 12 Volts (V). and the distance, d, between the plates is 0.03 meters (m). What is the electric field strength between them?
The negative sign indicates that the direction of the electric field is in the direction of decreasing potential, which is from the positive plate to the negative plate. However, for many practical calculations, we are only interested in the magnitude of the electric field.
Summary
Charges create an electric field.
Charged particles in an electric field experience force.
Coulomb's law tells us the force between two point charges:
F = k q1q2r2
The force a charged particle of strength q feels in electric field with local strength E is given by: F = qE
The work done W on a charge q that moves a distance d in an electric field with local strength E is: W = qEd
That formula can help us calculate the energy transferred when a charge is moved within an electric field, whether it be kinetic energy gained by accelerating charges or potential energy stored in a capacitor.
We can link the electric field E to the voltage V across a distance d using the formula E = -V/d
This helps us understand that electric fields can create potential differences, or voltage, across spaces in a circuit or between two plates of a capacitor.
Voltage V can also be understood through the work done W on a charge q by the formula V = W/q. It defines voltage as the energy difference per charge.
Fun Fact: Direction and Rate of Charge Flow
In a typical circuit, the flow of charge is from the positive terminal of the power source (such as a battery) towards the negative terminal. But actually it is the negatively charged electrons that move in the opposite direction, from the negative terminal towards the positive terminal.