Sam Loyd's Boxer's Puzzle - Solution
The Puzzle:
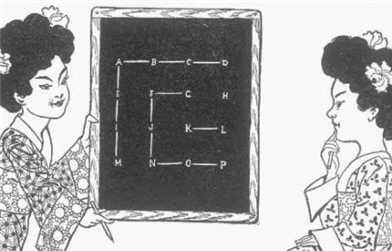
Here is an odd little puzzle-game from the East:
One of the Chinese girls writes sixteen letters on a slate in four rows, as shown, and after marking a straight dash, which connects A to B, passes the slate to her opponent, who connects E with A.
(Note: they are playing the Dots and Boxes Game, RP)
If the first player should now connect E with F the other player would connect B with F and score "one box", and have the right to play again.
But they have played so well that neither one has yet scored a box, although each has played six times, but the game is reaching a critical point where one of them must win, for there are no draws (for there are nine boxes altogether in this play) as in other games.
The little maiden sitting down has to play now, and if she connects M and N her opponent would score four boxes in one run, and then having the right to one more play would connect H and L, which would win all the rest.
What play would you now advise, and how many boxes will it win against the best possible play of the second player?
Our Solution:
There are many possible best moves.
One of the best moves is as follows: the first player would score seven boxes by beginning with a line from G to H. If the second player then marks from J to K, the first will score two boxes by marking from K to O and P to L, and will then play the waiting move, L to H, instead of scoring two more boxes.
The other player now scores the two boxes by G and K, and is then compelled to make a play which gives the first player five others. If, when the first player marks from G to H, the second player marks C-G, B-F, E-F, and then makes the waiting play of M-N, which scores four more boxes.
It is this sharp play of giving your opponent two boxes so as to then get four which constitutes the pretty points of the game.