Hyperbolic Functions
The two basic hyperbolic functions are "sinh" and "cosh":
Hyperbolic Sine:
sinh(x) = ex − e-x2
(pronounced "shine" or "sinch")
Hyperbolic Cosine:
cosh(x) = ex + e-x2
(pronounced "kosh")
They use the natural exponential function ex
They are not the same as sin(x) and cos(x), but a little bit similar:
sinh vs sin
cosh vs cos
Note: cosh(x) is always positive, and cosh(0)=1

Catenary
One of the interesting uses of Hyperbolic Functions is the curve made by suspended cables or chains.
A hanging cable forms a curve called a catenary defined using the cosh function:
f(x) = a cosh(x/a)
Like in this example from the page arc length :
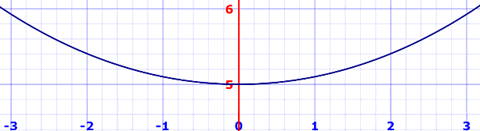
Here a is a positive constant: larger a makes the curve wider and flatter, and smaller a makes it narrower and steeper.
Other Hyperbolic Functions
From sinh and cosh we can create:
Hyperbolic tangent "tanh":
tanh(x) = sinh(x)cosh(x) = ex − e-xex + e-x
tanh vs tan
(pronounced "tanch" or "than")
Hyperbolic cotangent:
coth(x) = cosh(x)sinh(x) = ex + e-xex − e-x
not defined at x=0 because that would divide by 0
Hyperbolic secant:
sech(x) = 1cosh(x) = 2ex + e-x
Hyperbolic cosecant "csch" or "cosech":
csch(x) = 1sinh(x) = 2ex − e-x
not defined at x=0 because that would divide by 0
Why the Word "Hyperbolic" ?
Because it comes from measurements made on a Hyperbola:
So, just like the trigonometric functions relate to a circle, the hyperbolic functions relate to a hyperbola.
Identities
- sinh(−x) = −sinh(x)
- cosh(−x) = cosh(x)
And
- tanh(−x) = −tanh(x)
- coth(−x) = −coth(x)
- sech(−x) = sech(x)
- csch(−x) = −csch(x)
And the very important identity
- cosh2(x) − sinh2(x) = 1
(compare with cos2(x) + sin2(x) = 1)
Pronounciation Guide
People have a lot of fun pronouncing these functions!
| Function | Common Pronunciation | Rhymes With... |
|---|---|---|
| sinh(x) | "shine" or "sinch" | mine / pinch |
| cosh(x) | "kosh" | gosh |
| tanh(x) | "tanch" or "than" | ranch / ran |
| sech(x) | "seech" or "setch" | beach / fetch |
| csch(x) | "ko-seech" | (no direct rhyme) |
| coth(x) | "koth" | both (with a soft 'th') |
Odd and Even
Both cosh and sech are Even Functions, the rest are Odd Functions.
Derivatives
The Derivatives are:
ddx sinh(x) = cosh(x)
ddx cosh(x) = sinh(x)
ddx tanh(x) = 1 − tanh2(x)
