Logarithmic Function Reference

This is the Logarithmic Function:

f(x) = log_a(x)

a is any value greater than 0, except 1

When a=1, the graph is not defined

Apart from that there are two cases to look at:

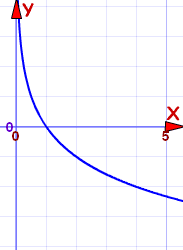
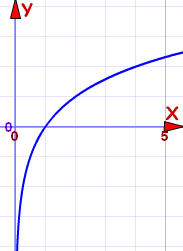
a between 0 and 1		a above 1

Example: f(x) = log_½(x)		Example: f(x) = log₂(x)
For a between 0 and 1 As x nears 0, it heads to infinity As x increases it heads to -infinity It is a Strictly Decreasing function It has a Vertical Asymptote along the y-axis (x=0).		For a above 1: As x nears 0, it heads to -infinity As x increases it heads to infinity it is a Strictly Increasing function It has a Vertical Asymptote along the y-axis (x=0).

Plot the graph here (use the "a" slider)

always has positive x, and never crosses the y-axis
always intersects the x-axis at x=1 ... in other words it passes through (1,0)
equals 1 when x=a, in other words it passes through (a,1)
is an Injective (one-to-one) function

Its Domain is the Positive Real Numbers: (0, +∞)

Its Range is the Real Numbers:

Inverse

So the Logarithmic Function can be "reversed" by the Exponential Function.

This is the "Natural" Logarithm Function:

f(x) = log_e(x)

Where e is "Eulers Number" = 2.718281828459... etc

But it is more common to write it this way:

f(x) = ln(x)

"ln" meaning "log, natural"

So when you see ln(x), just remember it is the logarithmic function with base e: log_e(x).

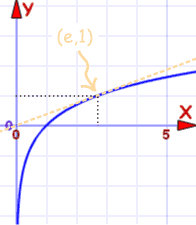
natural logarithm function
Graph of f(x) = ln(x)

At the point (e,1) the slope of the line is 1/e and the line is tangent to the curve.