Complex Number Multiplication

A Complex Number
A Complex Number is a combination of a Real and Imaginary Number:
A Real Number is the type of number we use every day.
Examples: 12.38, ½, 0, −2000
An Imaginary Number, when squared gives a negative result:
Examples: 5i, −3.6i, i/2,500i
Where "i" is the unit imaginary number
i2 = −1
Examples of Complex Numbers:
| 3.6 + 4i | (real part is 3.6, imaginary part is 4i) | |
| −0.02 + 1.2i | (real part is −0.02, imaginary part is 1.2i) | |
| 25 − 0.3i | (real part is 25, imaginary part is −0.3i) |
Either part can be zero:
| 0 + 2i | (no real part, imaginary part is 2i) | same as 2i | ||
| 4 + 0i | (real part is 4, no imaginary part) | same as 4 |
Multiplying
To multiply complex numbers:
Each part of the first complex number gets multiplied by
each part of the second complex number
Just use "FOIL", which stands for "Firsts, Outers, Inners, Lasts" (see Binomial Multiplication for more details):
|
|
|
(a+bi)(c+di) = ac + adi + bci + bdi2 |
|
Like this:
Example: (3 + 2i)(1 + 7i)
Here is another example:
Example: (1 + i)2
But There is a Quicker Way!
Use this rule:
(a+bi)(c+di) = (ac−bd) + (ad+bc)i
Example:
Why Does That Rule Work?
It is just the "FOIL" method after a little work:
| (a+bi)(c+di) | = | ac + adi + bci + bdi2 | FOIL method | |
| = | ac + adi + bci − bd | (because i2=−1) | ||
| = | (ac − bd) + (ad + bc)i | (gathering like terms) |
And there you have the (ac − bd) + (ad + bc)i pattern.
This rule is certainly faster, but if you forget it, just remember the FOIL method.
Now let's see what multiplication looks like on the Complex Plane.
The Complex Plane
| This is the complex plane: |
It is a plane for complex numbers! |
| We can plot a complex number like 3 + 4i :
It is placed
|
Multiplying By i
|
Let's multiply it by i: (3 + 4i) x i = 3i + 4i2
Which simplifies to (because i2 = −1): −4 + 3i |
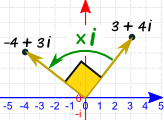 |
And here is the cool thing ... it's the same as rotating by a right angle (90° or π/2)
Was that just a weird coincidence?
Let's keep multiplying by i to see what happens:
Well, isn't that stunning? Each time it rotates by a right angle, until it ends up where it started.
Let's try it on the number 1:
|
 |
||||||||||||||||
Each time a right angle rotation.
Choose your own complex number and try that for yourself, it is good practice.
Let's look more closely at angles now.
Polar Form
| Our friendly complex number 3 + 4i : | ||
|
Here it is again, but in polar form: |
So the complex number 3 + 4i can also be shown as distance (5) and angle (0.927 radians).
How do we do the conversions?
Example: the number 3 + 4i
We can do a Cartesian to Polar conversion:
- r = √(x2 + y2) = √(32 + 42) = √25 = 5
- θ = tan-1 (y/x) = tan-1 (4/3) = 0.927 (to 3 decimals)
We can also take Polar coordinates and convert them to Cartesian coordinates:
- x = r × cos( θ ) = 5 × cos( 0.927 ) = 5 × 0.6002... = 3 (at perfect accuracy)
- y = r × sin( θ ) = 5 × sin( 0.927 ) = 5 × 0.7998... = 4 (at perfect accuracy)
In fact, a common way to write a complex number in Polar form is
| x + iy | = | r cos θ + i r sin θ |
| = | r(cos θ + i sin θ) |
And "cos θ + i sin θ" is often shortened to "cis θ", so:
x + iy = r cis θ
cis θ is just shorthand for cos θ + i sin θ
So we can write:3 + 4i = 5 cis 0.927
In some subjects, like electronics, "cis" is used a lot!
Now For Some More Multiplication
Let's try another multiplication:
Example: Multiply 1+i by 3+i
And here is the result on the Complex Plane:
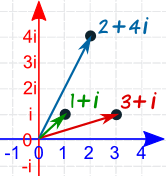
But it is more interesting to see those numbers in Polar Form:
Example: (continued)
Convert 1+i to Polar:
- r = √(12 + 12) = √2
- θ = tan-1 (1/1) = 0.785 (to 3 decimals)
Convert 3+i to Polar:
- r = √(32 + 12) = √10
- θ = tan-1 (1/3) = 0.322 (to 3 decimals)
Convert 2+4i to Polar:
- r = √(22 + 42) = √20
- θ = tan-1 (4/2) = 1.107 (to 3 decimals)
Have a look at the r values for a minute. Are they related somehow?
And what about the θ values?
Here is that multiplication in one line (using "cis"):
(√2 cis 0.785) × (√10 cis 0.322) = √20 cis 1.107
This is the interesting thing:
- √2 x √10 = √20
- 0.785 + 0.322 = 1.107
So:
The magnitudes get multiplied
and the angles get added
When multiplying in Polar Form: multiply the magnitudes, add the angles.
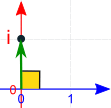
And that is why multiplying by i rotates by a right angle:
and forms a right angle on the complex plane
Squaring
To square a complex number, multiply it by itself:
- multiply the magnitudes: magnitude × magnitude = magnitude2
- add the angles: angle + angle = 2 , so we double them.
Result: square the magnitudes, double the angle.
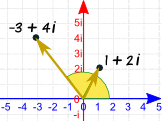
Example: Let us square 1 + 2i:
On the diagram the angle looks to be (and is!) doubled.
Also:
- The magnitude of (1+2i) = √(12 + 22) = √5
- The magnitude of (−3+4i) = √(32 + 42) = √25 = 5
So the magnitude got squared, too.
In general, a complex number like:
r(cos θ + i sin θ)
When squared becomes:
r2(cos 2θ + i sin 2θ)
The magnitude r gets squared and the angle θ gets doubled.
Or in the shorter "cis" notation:
(r cis θ)2 = r2 cis 2θ

De Moivre's Formula
We can make the previous formula more general! With the help of Abraham de Moivre we have a formula for any integer n:
(r cis θ)n = rn cis nθ
The magnitude becomes rn and the angle becomes nθ
Example: What is (1+i)6
First convert 1+i to Polar:
- r = √(12 + 12) = √2
- θ = tan-1 (1/1) = π/4
In "cis" notation is now: √2 cis π/4
Use the formula with an exponent of 6:
(√2 cis π/4)6 = (√2)6 cis 6π/4
Which simplifies to:
8 cis 3π/2
In other words: the magnitude is now 8, and the angle is 3π/2 (=270°)
Which is also 0−8i (see diagram)
Learn more at de Moivre's Formula
Summary
- Use "FOIL" to multiply complex numbers,
- Or use the formula:
(a+bi)(c+di) = (ac−bd) + (ad+bc)i
- Or use polar form and then multiply the magnitudes and add the angles.
- De Moivre's Formula can be used for integer exponents:
[ r(cos θ + i sin θ) ]n = rn(cos nθ + i sin nθ)
- Polar form r cos θ + i r sin θ is often shortened to r cis θ