Binary, Decimal and Hexadecimal Numbers
Decimals
How do Decimal Numbers work?
Every digit in a decimal number has a "position", and the decimal point helps us to know which position is which:
The position just left of the point is the "Ones" position. If we see a "7" there we know it means 7 ones.
Each position further left is worth 10 times more, and each position further right is worth 10 times less.
This is just a way of writing down a value.
Other ways include Roman Numerals, Binary, Hexadecimal and Tally Marks. Or we could simply draw dots on a sheet of paper!
Bases
The Decimal Number System is also called "Base 10", because it is based on the number 10, with these 10 symbols:
0, 1, 2, 3, 4, 5, 6, 7, 8 and 9
But notice something interesting: there is no symbol for "ten". "10" is actually two symbols put together, a "1" and a "0":
In decimal we count "0, 1, 2, 3, 4, 5, 6, 7, 8, 9,..." but then we run out of symbols!
So we add 1 on the left and then start again at 0: 10, 11, 12, ...
| 0 | Start at 0 | ||
| • | 1 | Then 1 | |
| •• | 2 | Then 2 | |
| ⋮ | |||
| ••••••••• | 9 | Up to 9 | |
| •••••••••• | 10 | Start back at 0 again, but add 1 on the left | |
| •••••••••• • |
11 | ||
| •••••••••• •• |
12 | ||
| ⋮ | |||
| •••••••••• ••••••••• |
19 | ||
| •••••••••• •••••••••• |
20 | Start back at 0 again, but add 1 on the left | |
| •••••••••• •••••••••• • |
21 | And so on! |
Counting with Different Number Systems
But we don't have to use 10 as a "Base". We could use 2 ("Binary"), 16 ("Hexadecimal"), or any number we want to!
Example: In binary we count "0, 1,..." but then we run out of symbols!
So we add 1 on the left and then start again at 0: 10, 11 ...
See how to count dots using Bases from 2 to 16 (press Play button):
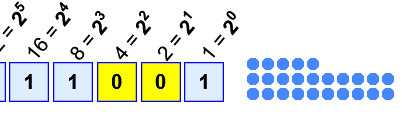
Example: 1×16 + 1×8 + 1×1 = 16+8+1 = 25
Try this: select a Base, watch it count for a while, then press "||" (Pause). Now see if it has tallied the right number of dots, as in this example using base 2.
So the general rule is:
Count up until just before the Base Number, then start at 0 again, but first add 1 to the number on our left.
So "10" means "one group of the base and zero ones".
- In base 2, "10" means two
- In base 10, "10" means ten
- In base 16, "10" means sixteen
Binary Numbers
Binary Numbers are just "Base 2" instead of "Base 10". So we start counting at 0, then 1, then we run out of digits ... so we start back at 0 again, but increase the number on the left by 1.
Like this:
| 0 | Start at 0 | ||
| • | 1 | Then 1 | |
| •• | 10 | there is no "2" in binary, so we start back at 0 ... ... and add one to the number on the left |
|
| ••• | 11 | ||
| •••• | 100 | start back at 0 again, and add one to the number on the left... ... but that number is already at 1 so it also goes back to 0 ... ... and 1 is added to the next position on the left |
|
| ••••• | 101 | ||
| •••••• | 110 | ||
| ••••••• | 111 | ||
| •••••••• | 1000 | Start back at 0 again (for all 3 digits), add 1 on the left |
|
| ••••••••• | 1001 | And so on! |
Hexadecimal Numbers
Hexadecimal numbers are interesting. There are 16 of them!
They look the same as the decimal numbers up to 9, but then there are the letters A, B, C, D, E and F in place of the decimal numbers 10 to 15.
So a single Hexadecimal digit can show 16 different values instead of the normal 10 like this:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hexadecimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
And we count in Hexadecimal like this:
| 0 | Start at 0 | ||
| • | 1 | Then 1 | |
| •• | 2 | Then 2 | |
| ⋮ | |||
| •••••••••• ••••• |
F | Up to F | |
| •••••••••• •••••• |
10 | Start back at 0 again, but add 1 on the left | |
| •••••••••• ••••••• |
11 | ||
| •••••••••• •••••••• |
12 | ||
| ⋮ | |||
| •••••••••• •••••••••• •••••••••• • |
1F | ||
| •••••••••• •••••••••• •••••••••• •• |
20 | Start back at 0 again, but add 1 on the left | |
| •••••••••• •••••••••• •••••••••• ••• |
21 | And so on! |
