How To Find if Triangles are Congruent

Two triangles are congruent if they have:

exactly the same three sides and
exactly the same three angles

But we don't have to know all three sides and all three angles ...usually three out of the six is enough.

There are five ways to find if two triangles are congruent: SSS, SAS, ASA, AAS and HL.

1. SSS (Side, Side, Side)

Two triangles with three corresponding sides marked with matching tick marks

SSS stands for "Side, Side, Side" and means that we have two triangles with all three sides equal.

For example:

is congruent to

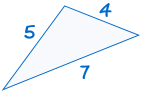
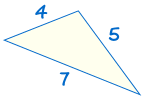
(See Solving SSS Triangles to discover more)

If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.

2. SAS (Side, Angle, Side)

Two triangles with two sides and the included angle marked as equal

SAS stands for "Side, Angle, Side" and means that we have two triangles where we know two sides and the included angle are equal.

For example:

is congruent to

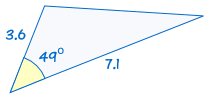
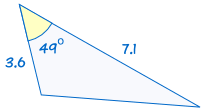
(See Solving SAS Triangles to discover more)

If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.

3. ASA (Angle, Side, Angle)

ASA Triangle

ASA stands for "Angle, Side, Angle" and means that we have two triangles where we know two angles and the included side are equal.

For example:

is congruent to

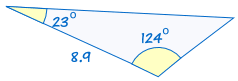
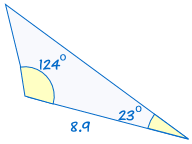
(See Solving ASA Triangles to discover more)

If two angles and the included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

4. AAS (Angle, Angle, Side)

AAS Triangle

AAS stands for "Angle, Angle, Side" and means that we have two triangles where we know two angles and the non-included side are equal.

For example:

is congruent to

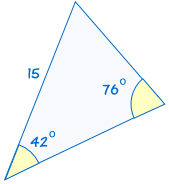
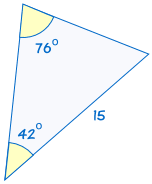
(See Solving AAS Triangles to discover more)

Why does this work? When we know two angles, the third angle is automatically fixed because all angles in a triangle add up to 180°. The known side then gives us the triangle's size.

If two angles and the non-included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

5. HL (hypotenuse, leg)

This one applies only to right triangles!

HL stands for "Hypotenuse, Leg" because the longest side of a right triangle is called the "hypotenuse" and the other two sides are called "legs".

It means we have two right triangles with

the same length of hypotenuse and
the same length for one of the other two legs

It doesn't matter which leg since the triangles could be rotated.

For example:

is congruent to

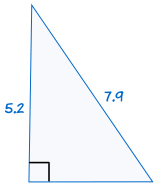
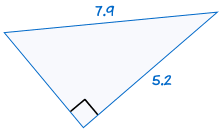
(See Pythagoras' Theorem to discover more)

If the hypotenuse and one leg of one right triangle are equal to the corresponding hypotenuse and leg of another right triangle, the two triangles are congruent.

Caution! Don't Use "SSA"

SSA stands for "Side, Side, Angle". This is where we know two sides and an angle that's not between them.

This generally doesn't work because there can be two different triangles that have the same SSA measurements.

Arc showing side b swinging to two possible intersection points on the base

Here we see an example with two possible values for A (see Solving SSA Triangles):

Caution! Don't Use "AAA"

AAA means we are given all three angles of a triangle, but no sides.

Two triangles of different sizes with identical angles

This isn't enough information to decide if two triangles are congruent!

Because the triangles can have the same angles but be different sizes:

is not congruent to:

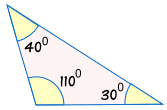
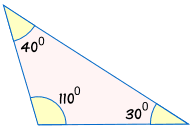
Without knowing at least one side, we can't be sure if two triangles are congruent.