How To Find if Triangles are Congruent

Two triangles are congruent if they have:

exactly the same three sides and
exactly the same three angles.

But we don't have to know all three sides and all three angles ...usually three out of the six is enough.

There are five ways to find if two triangles are congruent: SSS, SAS, ASA, AAS and HL.

1. SSS (side, side, side)

SSS Triangle

SSS stands for "side, side, side" and means that we have two triangles with all three sides equal.

For example:

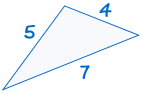is congruent to: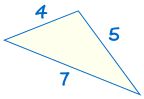

(See Solving SSS Triangles to find out more)

If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.

2. SAS (side, angle, side)

SAS Triangle

SAS stands for "side, angle, side" and means that we have two triangles where we know two sides and the included angle are equal.

For example:

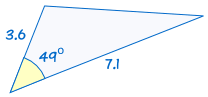is congruent to: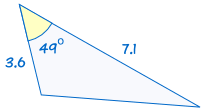

(See Solving SAS Triangles to find out more)

If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.

3. ASA (angle, side, angle)

ASA Triangle

ASA stands for "angle, side, angle" and means that we have two triangles where we know two angles and the included side are equal.

For example:

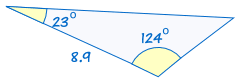is congruent to: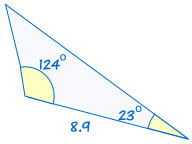

(See Solving ASA Triangles to find out more)

If two angles and the included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

4. AAS (angle, angle, side)

AAS Triangle

AAS stands for "angle, angle, side" and means that we have two triangles where we know two angles and the non-included side are equal.

For example:

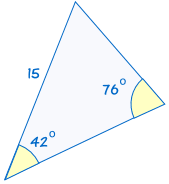is congruent to: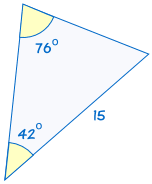

(See Solving AAS Triangles to find out more)

If two angles and the non-included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

5. HL (hypotenuse, leg)

This one applies only to right angled-triangles!

HL stands for "Hypotenuse, Leg" because the longest side of a right-angled triangle is called the "hypotenuse" and the other two sides are called "legs".

It means we have two right-angled triangles with

the same length of hypotenuse and
the same length for one of the other two legs.

It doesn't matter which leg since the triangles could be rotated.

For example:

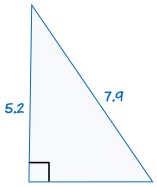is congruent to: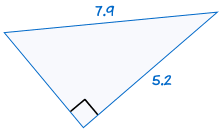

(See Pythagoras' Theorem to find out more)

If the hypotenuse and one leg of one right-angled triangle are equal to the corresponding hypotenuse and leg of another right-angled triangle, the two triangles are congruent.

Caution! Don't Use "AAA"

AAA means we are given all three angles of a triangle, but no sides.

AAA Triangle

This is not enough information to decide if two triangles are congruent!

Because the triangles can have the same angles but be different sizes:

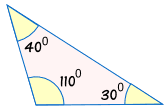is not congruent to: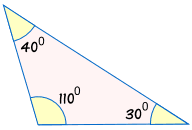

Without knowing at least one side, we can't be sure if two triangles are congruent.